题目内容
在空间直角坐标系O-xyz中,方程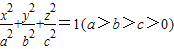 表示中心在原点、其轴与坐标轴重合的某椭球面的标准方程.2a,2b,2c分别叫做椭球面的长轴长,中轴长,短轴长.类比在平面直角坐标系中椭圆标准方程的求法,在空间直角坐标系O-xyz中,若椭球面的中心在原点、其轴与坐标轴重合,平面xOy截椭球面所得椭圆的方程为
表示中心在原点、其轴与坐标轴重合的某椭球面的标准方程.2a,2b,2c分别叫做椭球面的长轴长,中轴长,短轴长.类比在平面直角坐标系中椭圆标准方程的求法,在空间直角坐标系O-xyz中,若椭球面的中心在原点、其轴与坐标轴重合,平面xOy截椭球面所得椭圆的方程为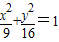 ,且过点
,且过点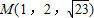 ,则此椭球面的标准方程为 .
,则此椭球面的标准方程为 .
【答案】分析:类比求曲线方程的方法,我们可以用坐标法,求空间坐标系中椭球面的方程.只须求出椭球面的长轴长,中轴长,短轴长,类比在平面直角坐标系中椭圆标准方程的求法,易得椭球面的方程.
解答:解:根据中心在原点、其轴与坐标轴重合的某椭球面的标准方程的定义,设此椭球面的标准方程为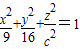 ,
,
∵且过点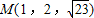 ,
,
将它的坐标代入椭球面的标准方程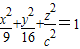 ,得
,得
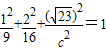 ,∴c2=36,
,∴c2=36,
故答案为: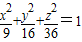
点评:类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).由于空间直角坐标系中椭球面标准方程与平面直角坐标系中椭圆标准方程相似,故我们可以利用求平面曲线方程的办法求解.
解答:解:根据中心在原点、其轴与坐标轴重合的某椭球面的标准方程的定义,设此椭球面的标准方程为
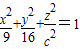 ,
,∵且过点
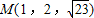 ,
,将它的坐标代入椭球面的标准方程
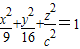 ,得
,得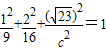 ,∴c2=36,
,∴c2=36,故答案为:
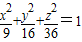
点评:类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).由于空间直角坐标系中椭球面标准方程与平面直角坐标系中椭圆标准方程相似,故我们可以利用求平面曲线方程的办法求解.

练习册系列答案
相关题目