题目内容
设数列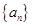 的前n项和
的前n项和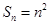 ,数列
,数列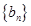 满足
满足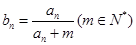 .
.
(1)若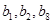 成等比数列,试求
成等比数列,试求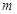 的值;
的值;
(2)是否存在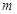 ,使得数列
,使得数列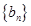 中存在某项
中存在某项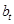 满足
满足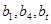 (
(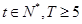 )成等差数列?若存在,请指出符合题意的
)成等差数列?若存在,请指出符合题意的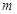 的个数;若不存在,请说明理由.
的个数;若不存在,请说明理由.
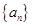 的前n项和
的前n项和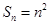 ,数列
,数列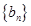 满足
满足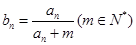 .
.(1)若
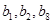 成等比数列,试求
成等比数列,试求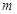 的值;
的值;(2)是否存在
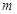 ,使得数列
,使得数列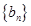 中存在某项
中存在某项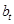 满足
满足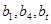 (
(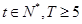 )成等差数列?若存在,请指出符合题意的
)成等差数列?若存在,请指出符合题意的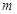 的个数;若不存在,请说明理由.
的个数;若不存在,请说明理由.(1)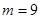 ;(2)存在在9个
;(2)存在在9个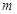 的值满足要求.
的值满足要求.
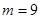 ;(2)存在在9个
;(2)存在在9个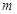 的值满足要求.
的值满足要求.试题分析:(1)由前n项和求通项,根据
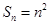 ,可求
,可求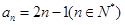
代入求得
 ,进一步求得,
,进一步求得,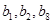 的值,由
的值,由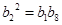 ,可求得
,可求得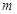 的值.
的值. (2)先假设存在
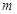 使得
使得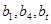 (
(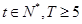 )成等差数列,得
)成等差数列,得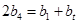 ,则
,则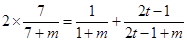 ,化简得
,化简得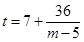 ,由
,由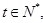 可以求得符合题意得m值。
可以求得符合题意得m值。试题解析:
(1)因为
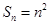 ,所以当
,所以当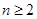 时,
时,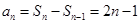
又当
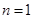 时,
时,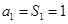 ,适合上式,所以
,适合上式,所以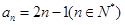 ,所以
,所以 ,则
,则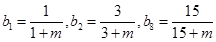 ,由
,由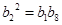 ,得
,得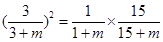 ,解得
,解得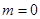 (舍)或
(舍)或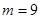 ,所以
,所以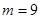
(2)假设存在
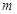 ,使得
,使得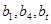 (
(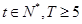 )成等差数列,即
)成等差数列,即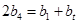 ,则
,则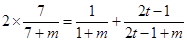 ,化简得
,化简得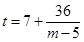
所以当m-5=1,2,3,4,6,9,12,18,36时,分别存在t =43,25,19,16,13,11,10,9,8适合题意,即存
在这样m,且符合题意的m共有9个.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
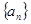 中,
中, ,求数列
,求数列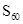
 时,数列{an}为递减数列;②当
时,数列{an}为递减数列;②当 为正整数时,数列{an}必有两项相等的最大项
为正整数时,数列{an}必有两项相等的最大项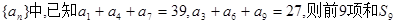 的值为( )
的值为( ) 前项和为
前项和为 ,且点
,且点 在
在 图像上,求
图像上,求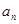
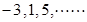 的第15项为( )
的第15项为( ) 中,
中,
 ,则此数列前30项和等于( )
,则此数列前30项和等于( )