题目内容
定义:对于两个双曲线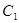 ,
,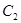 ,若
,若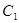 的实轴是
的实轴是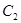 的虚轴,
的虚轴,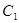 的虚轴是
的虚轴是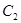 的实轴,则称
的实轴,则称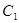 ,
,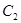 为共轭双曲线.现给出双曲线
为共轭双曲线.现给出双曲线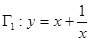 和双曲线
和双曲线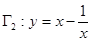 ,其离心率分别为
,其离心率分别为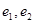 .
.
(1)写出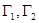 的渐近线方程(不用证明);
的渐近线方程(不用证明);
(2)试判断双曲线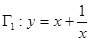 和双曲线
和双曲线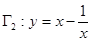 是否为共轭双曲线?请加以证明.
是否为共轭双曲线?请加以证明.
(3)求值: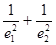 .
.
(1)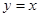 、
、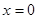 ;(2)是;(3)1.
;(2)是;(3)1.
解析试题分析:(1)由其图像很容易知道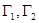 的渐近线方程即
的渐近线方程即 轴和一、三象限的角平分线.从而写出
轴和一、三象限的角平分线.从而写出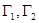
的渐近线方程都是: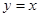 和
和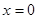 ;(2)先利用渐近线与实轴、虚轴间的关系得到
;(2)先利用渐近线与实轴、虚轴间的关系得到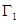 的实轴所在直线为
的实轴所在直线为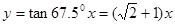 与虚轴所在直线为
与虚轴所在直线为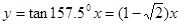 .然后计算实轴与双曲线
.然后计算实轴与双曲线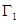
的交点,从而得到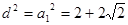 、
、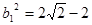 、
、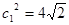 .同理也可得到
.同理也可得到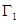 的类似数据,从
的类似数据,从
而得到证明;(3)由上问即可得到 ,
,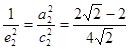 ,所以
,所以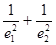 ="1" .
="1" .
试题解析:(1)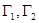 的渐近线方程都是:
的渐近线方程都是: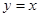 和
和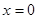 . 3分
. 3分
(2)双曲线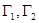 是共轭双曲线. 4分
是共轭双曲线. 4分
证明如下: 对于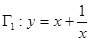 ,实轴和虚轴所在的直线是
,实轴和虚轴所在的直线是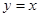 和
和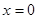 的角平分线所
的角平分线所
的直线, 所以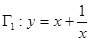 的实轴所在直线为
的实轴所在直线为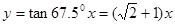 ,
,
虚轴所在直线为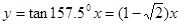 , 6分
, 6分
实轴 和
和 的交点
的交点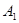 到原点的距离的平方
到原点的距离的平方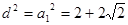 .
.
又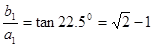 ,所以
,所以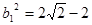 从而得
从而得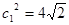 ; 8分
; 8分
同理对于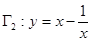 ,实轴所在直线为
,实轴所在直线为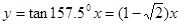 ,
,
虚轴所在直线为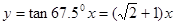 ,
,
实轴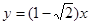 和
和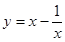 的交点
的交点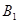 到原点的距离的平方
到原点的距离的平方
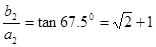 ,所以
,所以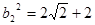 ,从而得
,从而得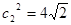 .
.
综上所述,双曲线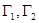 是共轭双曲线. 10分
是共轭双曲线. 10分
(3) 由(2)易得 ,
,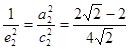 ,
,
所以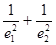 ="1" . 13分
="1" . 13分
考点:1.双曲线的几何性质;2.共轭双曲线的定义;3.离心率.

练习册系列答案
相关题目
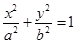
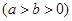 上的点到其两焦点距离之和为
上的点到其两焦点距离之和为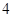 ,且过点
,且过点 .
. 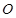 为坐标原点,斜率为
为坐标原点,斜率为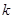 的直线过椭圆的右焦点,且与椭圆交于点
的直线过椭圆的右焦点,且与椭圆交于点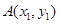 ,
,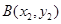 ,若
,若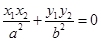 ,求△
,求△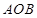 的面积.
的面积.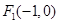 、
、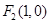 为椭圆
为椭圆 的左、右焦点,且点
的左、右焦点,且点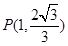 在椭圆
在椭圆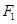 的直线
的直线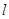 交椭圆
交椭圆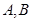 两点,则
两点,则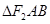 的内切圆的面积是否存在最大值?
的内切圆的面积是否存在最大值? 的中心在原点,焦点在
的中心在原点,焦点在 轴上,长轴长为
轴上,长轴长为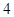 ,且点
,且点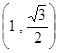 在椭圆
在椭圆 是椭圆
是椭圆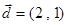 的直线
的直线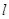 交椭圆
交椭圆 、
、 两点,求证:
两点,求证: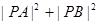 为定值.
为定值.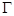 :
: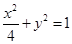 .
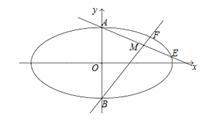
.
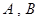 (如图),直线
(如图),直线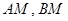 分别与椭圆
分别与椭圆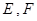 两点,其中点
两点,其中点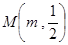 满足
满足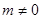 ,且
,且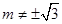 .
.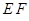 与
与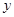 轴交点的位置与
轴交点的位置与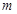 无关;
无关;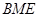 面积是∆
面积是∆ 面积的5倍,求
面积的5倍,求 :
: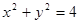 .
.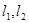 是过点
是过点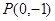 的两条互相垂直的直线,其中
的两条互相垂直的直线,其中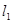 交圆
交圆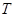 、
、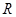 两点,
两点,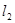 交椭圆
交椭圆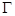 于另一点
于另一点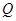 .求
.求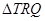 面积取最大值时直线
面积取最大值时直线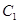 的方程为
的方程为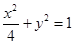 ,双曲线
,双曲线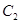 的左、右焦点分别为
的左、右焦点分别为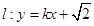 与椭圆
与椭圆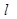 与
与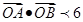 (其中0为原点),求k的取值范围。
(其中0为原点),求k的取值范围。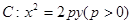 的焦点为
的焦点为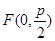 ,准线为
,准线为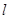 ,点
,点 为抛物线C上的一点,且
为抛物线C上的一点,且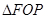 的外接圆圆心到准线的距离为
的外接圆圆心到准线的距离为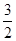 .
.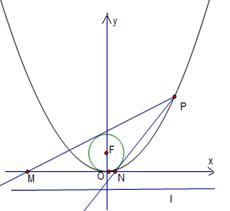
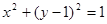 ,过点P作圆F的2条切线分别交
,过点P作圆F的2条切线分别交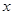 轴于点
轴于点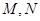 ,求
,求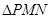 面积的最小值时
面积的最小值时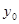 的值.
的值.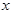 轴对称,它的顶点在坐标原点,点P(1,2),
轴对称,它的顶点在坐标原点,点P(1,2),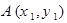 ,
,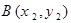 均在抛物线上.
均在抛物线上.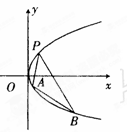
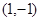 ,求直线AB方程.
,求直线AB方程.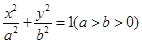 的离心率
的离心率 ,连接椭圆的四个顶点得到的菱形的面积为4.
,连接椭圆的四个顶点得到的菱形的面积为4.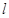 与椭圆相交于不同的两点A,B。已知点A的坐标为
与椭圆相交于不同的两点A,B。已知点A的坐标为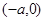 。若
。若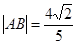 ,求直线
,求直线