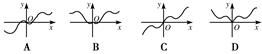题目内容
已知函数f(x)=lnx-a2x2+ax(a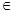 R).
R).
(l)当a=1时,证明:函数f(x)只有一个零点;
(2)若函数f(x)在区间(1,十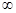 )上是减函数,求实数a的取值范围.
)上是减函数,求实数a的取值范围.
 R).
R).(l)当a=1时,证明:函数f(x)只有一个零点;
(2)若函数f(x)在区间(1,十
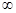 )上是减函数,求实数a的取值范围.
)上是减函数,求实数a的取值范围.(1)证明过程详见解析;(2)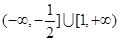
试题分析:本题主要考查导数的运算、利用导数研究函数的单调性及最值问题等数学知识,考查学生的转化能力、分析问题解决问题的能力和计算能力,考查分类讨论思想.第一问,将
 代入确定的解析式,先求函数的定义域,这是解题的前题,函数
代入确定的解析式,先求函数的定义域,这是解题的前题,函数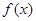 只有一个零点等价于
只有一个零点等价于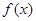 图像与x轴只有一个交点,对
图像与x轴只有一个交点,对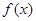 求导,利用
求导,利用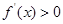 ,
,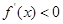 判断函数的增减区间,判断出当
判断函数的增减区间,判断出当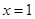 时,
时,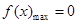 ,从而证明出
,从而证明出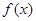 图像与x轴只有一个交点;第二问,对
图像与x轴只有一个交点;第二问,对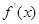 中的参数a进行讨论,当
中的参数a进行讨论,当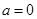 时,
时,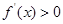 与题干矛盾,当
与题干矛盾,当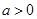 时,得到的减区间为
时,得到的减区间为 ,由题干分析可知,
,由题干分析可知,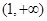 是
是 的子集,所以得到
的子集,所以得到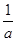 和1的大小关系,当
和1的大小关系,当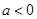 时,同理得到
时,同理得到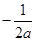 与1的大小,从而综合上述情况得到a的取值范围.
与1的大小,从而综合上述情况得到a的取值范围.试题解析:(1)当a=1时,f(x)=lnx-x2+x,其定义域是(0,+∞),
又
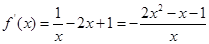 ,
,令f′(x)=0,即
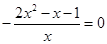 ,解得
,解得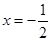 或x=1.又x>0,∴x=1.
或x=1.又x>0,∴x=1.当0<x<1时,f′(x)>0;当x>1时,f′(x)<0.
∴函数f(x)在区间(0,1)上单调递增,在区间(1,+∞)上单调递减.
∴当x=1时,函数f(x)取得最大值,其值为f(1)=ln1-12+1=0.
当x≠1时,f(x)<f(1),即f(x)<0.
∴函数f(x)只有一个零点.(7分)
(2)显然函数f(x)=lnx-a2x2+ax的定义域为(0,+∞),
∴
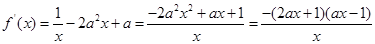 .
.①当a=0时,
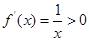 ,∴f(x)在区间(1,+∞)上为增函数,不合题意;
,∴f(x)在区间(1,+∞)上为增函数,不合题意;②当a>0时,f′(x)<0,得
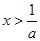 ,∴
,∴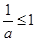 ,即a≥1;
,即a≥1;③当a<0时,f′(x)<0,得
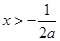 ,∴
,∴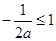 ,a≤-2.
,a≤-2.综上,实数a的取值范围是
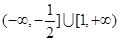 .(14分)
.(14分)
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
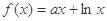 ,其中a为常数.
,其中a为常数. 时,求
时,求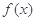 的最大值;
的最大值;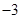 ,求a的值;
,求a的值;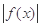 =
=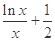 是否有实数解.
是否有实数解. 内的函数
内的函数 ,若对任意的
,若对任意的 都有
都有 ,则称函数
,则称函数 ,(
,( )是否为“妈祖函数”?如果是,请给出证明;如果不是,请说明理由.
)是否为“妈祖函数”?如果是,请给出证明;如果不是,请说明理由. .
. 时,求
时,求 的最大值;
的最大值; 恒成立;
恒成立; .(参考数据:
.(参考数据: )
)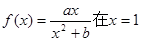 处取得极值2
处取得极值2 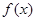 的表达式;
的表达式;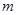 满足什么条件时,函数
满足什么条件时,函数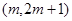 上单调递增?
上单调递增?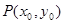 为
为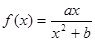 图象上任意一点,直线与
图象上任意一点,直线与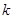 的取值范围
的取值范围 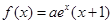 (其中
(其中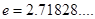 ),
),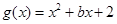 ,已知它们在
,已知它们在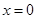 处有相同的切线.
处有相同的切线.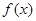 ,
,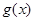 的解析式;
的解析式; 上的最小值;
上的最小值;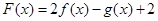 零点个数.
零点个数.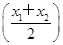 >0.
>0. 的导函数为f¢(x),则f¢(1)的值为 .
的导函数为f¢(x),则f¢(1)的值为 .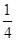 x2+
x2+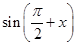 ,f′(x)为f(x)的导函数,则f′(x)的图象是( )
,f′(x)为f(x)的导函数,则f′(x)的图象是( )