题目内容
已知函数y=f(x)的图象是自原点出发的一第折线。当n≤y≤n+1(n=0,1,2…)时,该图象是斜率为bn的线段(其中正常数b≠1),设数列(1)求x1、x2和xn的表达式
(2)求f(x)的表达式,并写出其定义域;
(3)证明:y=f(x)的图像与y=x的图象没有横坐标大于1的交点。
答案:
解析:
解析:
| (1)依题意f(0)=0,又由f(x1)=1,当0≤y≤1时,函数y=f(x)的图象是斜率b0=1的线段,故由 又由f(x2)=2,当1≤y≤2时,函数y=f(x)的图象是斜率为b的线段, 故由 设当k-1≤y≤k时,xk=1+ (2)略。 (3)假设y=f(x)的图象与y=x的图象有大于1的交点,且xn<x≤xn+1(n∈N),则方程组 消去y得x=n+bn(x-xn),整理得(x-xn)(bn-1)=xn-n。(1),当b>1时,bn-1>0,x-xn>0,∴(x-xn)(bn-1)>0。 又∵ 即(1)左右不等,矛盾。其次,当b<1时,仿上述证明,也可导致矛盾。故函数y=f(x)的图象与y=x的图象没有横坐标大于l的交点。 |

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
已知函数y=f(x+
)为奇函数,设g(x)=f(x)+1,则g(
)+g(
)+g(
)+g(
)+…+g(
)=( )
| 1 |
| 2 |
| 1 |
| 2011 |
| 2 |
| 2011 |
| 3 |
| 2011 |
| 4 |
| 2011 |
| 2010 |
| 2011 |
| A、1005 | B、2010 |
| C、2011 | D、4020 |
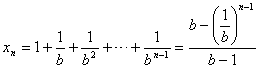 ;
;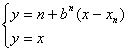 有解。
有解。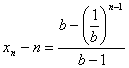
 。
。