题目内容
5.已知数集A={a,b,c,d},且a,b,c,d都是实数,数组x,y,z,t是集合A中四个元素的某一排列.设m=(x-y)2+(y-z)2+(z-t)2+(t-x)2的所有值构成集合B,那么集合B的元素个数是( )| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
分析 由m=(x-y)2+(y-z)2+(z-t)2+(t-x)2=2(x2+y2+z2+t2)-2(x+z)(y+t)可得:(x+z)(y+t)取不同值的个数,即为B中元素个数,进而利用排列组合公式得到答案.
解答 解:∵m=(x-y)2+(y-z)2+(z-t)2+(t-x)2
=2(x2+y2+z2+t2)-2(xy+yz+zt+tx),
=2(x2+y2+z2+t2)-2(x+z)(y+t),
故(x+z)(y+t)取不同值的个数,即为B中元素个数,
而数组x,y,z,t是集合A中四个元素的某一排列.
故共有$\frac{{C}_{4}^{2}}{{A}_{2}^{2}}$=3个,
故选:B.
点评 本题考查的知识点是集合中元素个数的最值,其中正确理解(x+z)(y+t)取不同值的个数,即为B中元素个数,是解答的关键.

练习册系列答案
相关题目
14.设U是全集,集合A、B满足A$\stackrel{?}{≠}$B,则下列命题不成立的是( )
| A. | A∪B=B | B. | A∩B=A | C. | A∪(CUB)=U | D. | (CUA)∪B=U |
15.设a,b为实数,若复数$\frac{1+2i}{a+bi}$=1+i,则( )
| A. | a=1,b=3 | B. | a=3,b=1 | C. | a=$\frac{1}{2}$,b=$\frac{3}{2}$ | D. | a=$\frac{3}{2}$,b=$\frac{1}{2}$ |
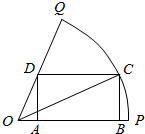 如图,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,C是扇形弧上的运动点,ABCD是扇形的内接矩形.记∠COP=α,求当角α取何值时,矩形ABCD的面积最大?并求出这个最大面积.
如图,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,C是扇形弧上的运动点,ABCD是扇形的内接矩形.记∠COP=α,求当角α取何值时,矩形ABCD的面积最大?并求出这个最大面积.