题目内容
若p是真命题,q是假命题。以下四个命题 ① p且q ② p或q ③ 非p ④非q。
其中假命题的个数是( )
| A.1 | B.2 | C.3 | D.4 |
B
解析试题分析:根据简单命题组成的复合命题的真值表可知,由于p是真命题,q是假命题,那么可知① p且q只有都为真命题才是真命题,故为假命题, ② p或q,只要有一个真命题即为真,因此是真命题。 ③ 因为p是真命题,则非p 假命题, ④,因为q是假命题,则非q是真命题,故真命题的个数为2个,选B
考点:本试题主要考查了复合命题的真值问题的运用。
点评:解决该试题的关键是根据且命题,一真即真,或命题,一假即假,而命题的否定和原命题中必有一个真的。

练习册系列答案
相关题目
设 则“
则“ 且
且 ”是“
”是“ ”的
”的
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.即不充分也不必要条件 |
“ ”是“
”是“ ”的( )
”的( )
| A.充要条件 | B.必要而不充分条件 |
| C.充分而不必要条件 | D.既不充分也不必要 |
在 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知 :函数
:函数 与
与 轴有两个交点;
轴有两个交点; :
: ,
, 恒成立.若
恒成立.若 为真,则实数m的取值范围为 ( )
为真,则实数m的取值范围为 ( )
A. | B. |
C. | D. |
“ ”是“函数
”是“函数 在其定义域上为奇函数”的( )
在其定义域上为奇函数”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
若命题“ 或
或 ”为真,“非p”为真,则( )
”为真,“非p”为真,则( )
| A.p真q真 | B.p假q真 | C.p真q假 | D.p假q假 |
下列命题中,真命题是( )
A.若 则 则 |
B.若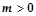 则 则 有实根 有实根 |
C.存在实数 当 当 时 时 |
D. 是 是 或 或 的充分不必要条件 的充分不必要条件 |
 ,则
,则 ”的否命题是“若
”的否命题是“若 ”
” :
: ,使
,使 ,则
,则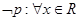 ,使
,使
 为假命题,则
为假命题,则 是函数
是函数 为偶函数的充要条件
为偶函数的充要条件