题目内容
“ ”是“函数
”是“函数 在其定义域上为奇函数”的( )
在其定义域上为奇函数”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
A
解析试题分析:当 时,
时,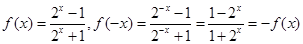 ,所以在其定义域上为奇函数;反之,若函数
,所以在其定义域上为奇函数;反之,若函数 在其定义域上为奇函数,则
在其定义域上为奇函数,则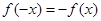 ,即
,即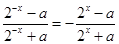 ,解得
,解得 ,所以“
,所以“ ”是“函数
”是“函数 在其定义域上为奇函数”的充分不必要条件.
在其定义域上为奇函数”的充分不必要条件.
考点:本小题主要考查函数的奇偶性的判断与应用、充分条件和必要条件,考查学生的运算求解能力和分析问题的能力.
点评:函数奇偶性的判断和应用关键在定义,只要深刻理解定义的内涵和外延,就能轻松解决该部分的高考试题.

练习册系列答案
相关题目
下列命题为特称命题的是()
| A.偶函数的图象关于y轴对称 | B.正四棱柱都是平行六面体 |
| C.不相交的两条直线是平行直线 | D.存在实数大于等于3 |
若p是真命题,q是假命题。以下四个命题 ① p且q ② p或q ③ 非p ④非q。
其中假命题的个数是( )
| A.1 | B.2 | C.3 | D.4 |
“ ”是“
”是“ ”的( ).
”的( ).
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
命题p:|x|<1,命题q: ,则
,则 是
是 成立的( )
成立的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
命题 ,使
,使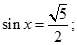 命题
命题 ,都有
,都有 给出下列结论:
给出下列结论:
① 命题“ ”是真命题 ② 命题“
”是真命题 ② 命题“ ”是假命题
”是假命题
③ 命题“ ”是真命题; ④ 命题“
”是真命题; ④ 命题“ ”是假命题
”是假命题
其中正确的是
| A.② ④ | B.② ③ | C.③ ④ | D.① ② ③ |
设 ,则“
,则“ ”是“直线
”是“直线 与直线
与直线 平行”的
平行”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
 ”是“
”是“ ”的 ( )
”的 ( ) 与集合
与集合 是同一个集合;
是同一个集合; 这些数组成的集合有
这些数组成的集合有 个元素;
个元素; 是指第二和第四象限内的点集。
是指第二和第四象限内的点集。 个
个  个
个  个
个  个
个