题目内容
已知 :函数
:函数 与
与 轴有两个交点;
轴有两个交点; :
: ,
, 恒成立.若
恒成立.若 为真,则实数m的取值范围为 ( )
为真,则实数m的取值范围为 ( )
A. | B. |
C. | D. |
C
解析试题分析:因为 :函数
:函数 与
与 轴有两个交点;则说明了其
轴有两个交点;则说明了其 =0的方程中判别式大于零,即为m2-4>0,解得m>2或,m<-2
=0的方程中判别式大于零,即为m2-4>0,解得m>2或,m<-2 :
: ,
, 恒成立.则说明开口向上,只有判别式小于零成立,故有16(m-2)2-16<0,1<m<3,则
恒成立.则说明开口向上,只有判别式小于零成立,故有16(m-2)2-16<0,1<m<3,则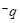 表示的集合为m
表示的集合为m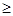 3,或m
3,或m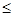 1,
1,
若 为真,则说明p和
为真,则说明p和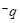 都是真的,那么利用交集思想得到
都是真的,那么利用交集思想得到 ,选C.
,选C.
考点:本试题主要考查了二次函数的图像与性质的综合运用。
点评:解决该试题的关键是理解二次函数与x轴有两个交点即为判别式大于零,而对于一切实数一元二次不等式恒成立的问题,主要是考虑二次项系数是否为零,以及判别式小于零时的情况即可。

练习册系列答案
相关题目
已知命题 : 双曲线的离心率小于1. 则
: 双曲线的离心率小于1. 则 为
为
| A.双曲线的离心率大于1 | B.有的双曲线离心率小于1 |
| C.有的双曲线离心率大于1 | D.存在双曲线, 其离心率不小于1 |
已知P: ,Q:
,Q: , 则下列判断正确的是( )
, 则下列判断正确的是( )
A.“P或Q”为真,“ p”为真 p”为真 | B.“P或Q”为假,“ p”为真 p”为真 |
C.“P且Q”为真,“ p”为假 p”为假 | D.“P且Q”为假,“ p”为假 p”为假 |
若p是真命题,q是假命题。以下四个命题 ① p且q ② p或q ③ 非p ④非q。
其中假命题的个数是( )
| A.1 | B.2 | C.3 | D.4 |
命题p:|x|<1,命题q: ,则
,则 是
是 成立的( )
成立的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
若命题“ ”为假,且“
”为假,且“ ”为假,则( )
”为假,则( )
A. 或 或 为假 为假 | B. 假 假 |
C. 真 真 | D.不能判断 的真假 的真假 |
设 ,
, ,则 “
,则 “ ”是“
”是“ ”的( )
”的( )
| A.充分但不必要条件 | B.必要但不充分条件 |
| C.充要条件 | D.既不充分也不必要的条件 |
 ”的否定是_ ;
”的否定是_ ; ,给出下列四个命题:
,给出下列四个命题: 时,
时, 是奇函数 ②
是奇函数 ②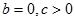 时,方程
时,方程 只有一个实根
只有一个实根 对称 ④方程
对称 ④方程