题目内容
(2012•广东模拟)在实数的原有运算法则中,定义新运算a?b=3a-b,则|x?(4-x)|+|(1-x)?x|>8的解集为
{x|x<-
,x>
}
| 1 |
| 8 |
| 15 |
| 8 |
{x|x<-
,x>
}
.| 1 |
| 8 |
| 15 |
| 8 |
分析:根据定义新运算a?b=3a-b,原不等式化为|x-1|+|x-
|>2,转化为与之等价的三个不等式组,分别解出这三个不等式组的解集,再把这三个解集取并集,即得所求.
| 3 |
| 4 |
解答:解:|x?(4-x)|+|(1-x)?x|>8,即|3x-(4-x)|+|3(1-x)-x|>8,即|4x-4|+|3-4x|>8,
即|x-1|+|x-
|>2.
∴①
,或②
,或 ③
.
解①得 x<-
. 解②得 x∈∅.解③得 x>
.
综上,不等式的解集为 {x|x<-
,x>
},
故答案为 {x|x<-
,x>
}.
即|x-1|+|x-
| 3 |
| 4 |
∴①
|
|
|
解①得 x<-
| 1 |
| 8 |
| 15 |
| 8 |
综上,不等式的解集为 {x|x<-
| 1 |
| 8 |
| 15 |
| 8 |
故答案为 {x|x<-
| 1 |
| 8 |
| 15 |
| 8 |
点评:本题主要考查定义新运算a?b=3a-b,绝对值不等式的解法,关键是去掉绝对值,化为与之等价的不等式组来解.体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
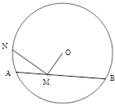 (2012•广东模拟)(几何证明选讲选做题)如图,点M为⊙O的弦AB上的一点,连接MO.MN⊥OM,MN交圆于N,若MA=2,MB=4,则MN=
(2012•广东模拟)(几何证明选讲选做题)如图,点M为⊙O的弦AB上的一点,连接MO.MN⊥OM,MN交圆于N,若MA=2,MB=4,则MN=