题目内容
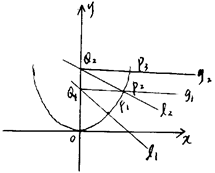
已知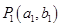 是曲线C:
是曲线C: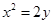 上的一点(其中
上的一点(其中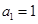 ),过点
),过点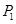 作与曲线C在
作与曲线C在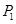 处的切线垂直的直线
处的切线垂直的直线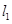 交
交 轴于点
轴于点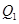 ,过
,过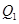 作与
作与 轴垂直的直线
轴垂直的直线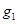 与曲线C在第一象限交于点
与曲线C在第一象限交于点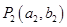 ;再过点
;再过点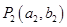 作与曲线C在
作与曲线C在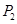 处的切线垂直的直线
处的切线垂直的直线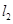 交轴于点
交轴于点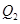 ,过
,过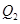 作与
作与 轴垂直的直线
轴垂直的直线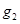 与曲线C在第一象限交于点
与曲线C在第一象限交于点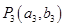 ;如此继续下去,得一系列的点
;如此继续下去,得一系列的点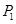 、
、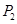 、、
、、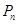 、。(其中
、。(其中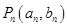 )
)
(1)求数列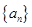 的通项公式。
的通项公式。
(2)若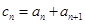 ,且
,且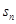 是数列
是数列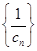 的前
的前 项和,
项和,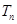 是数列
是数列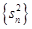 的前
的前 项
项
(1)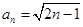 .(2)详见解析.
.(2)详见解析.
解析试题分析:(1)根据条件先找出数列中相邻项间的关系,即递推公式,然后利用递推公式求通项公式.
(2)由(1)可得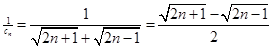 ,由此可求出
,由此可求出 ,
,
这个数列的和就不可能求出来了,怎么办?一般地,不能求和,就先放缩.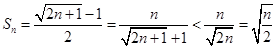 ,将此不等式平方再相加,右边就属于等差数列的和,用公式即可求出它的和.
,将此不等式平方再相加,右边就属于等差数列的和,用公式即可求出它的和.
试题解析:(1)由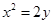 得
得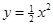 ,求导有
,求导有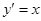 1分
1分
所以 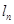 :
: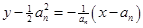 ,
,
令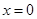 ,得
,得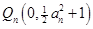 ,所以
,所以 ,
,
即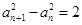 4分
4分
又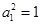 ,得
,得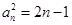 ,即
,即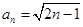 6分
6分
(2)∵ 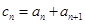
∴ 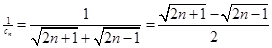 7分
7分
得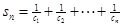
=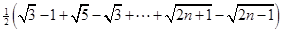
=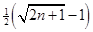 8分
8分
=
<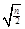 10分
10分
∴ 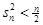 11分
11分
∴ 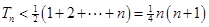 12分
12分
考点:数列与不等式.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
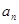 }是等差数列,其中每一项及公差
}是等差数列,其中每一项及公差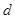 均不为零,设
均不为零,设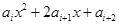 =0(
=0(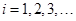 )是关于
)是关于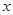 的一组方程.
的一组方程.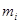 ,求证
,求证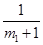 ,
,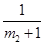 ,
,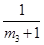 ,…,
,…, 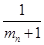 ,…也成等差数列.
,…也成等差数列. 中,公比
中,公比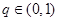 ,
, 且
且 和
和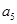 的等比中项是
的等比中项是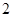 .
.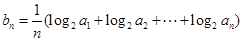 ,判断数列
,判断数列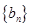 的前
的前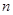 项和
项和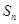 是否存在最大值,若存在,求出使
是否存在最大值,若存在,求出使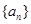 的前
的前 项和
项和 满足
满足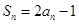
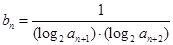 ;求数列
;求数列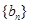 的前
的前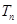 .
.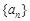 的首项
的首项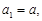 其中
其中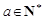 ,
,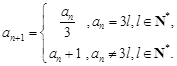 ,令集合
,令集合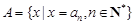 .
.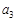 是数列
是数列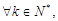 恒有
恒有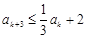 成立;
成立;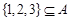 .
.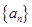 中,
中,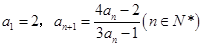 ,设
,设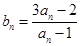 .
.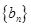 的前三项;
的前三项;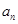 ;
;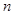 项和为
项和为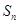 ,
,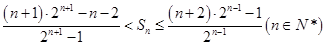 .
.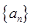 是等比数列,首项
是等比数列,首项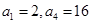 .
.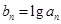 ,证明数列
,证明数列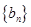 是等差数列并求前n项和
是等差数列并求前n项和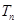 .
.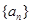 的前
的前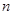 项和为
项和为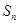 ,常数
,常数 ,且
,且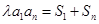 对一切正整数
对一切正整数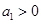 ,
,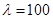 ,当
,当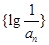 的前
的前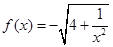 ,点
,点 在曲线
在曲线 上
上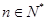 ,
,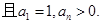 (Ⅰ)(Ⅰ)求数列
(Ⅰ)(Ⅰ)求数列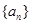 的通项公式;
的通项公式;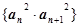 的前n项和为
的前n项和为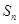 ,若对于任意的
,若对于任意的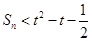 恒成立,求最小正整数t的值.
恒成立,求最小正整数t的值.