题目内容
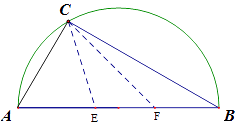
【题目】如图,有一直径为8米的半圆形空地,现计划种植果树,但需要有辅助光照.半圆周上的C处恰有一可旋转光源满足果树生长的需要,该光源照射范围是 ![]() ,点E,F在直径AB上,且
,点E,F在直径AB上,且 ![]() .
. 
(1)若 ![]() ,求AE的长;
,求AE的长;
(2)设∠ACE=α,求该空地种植果树的最大面积.
【答案】
(1)解:由已知得△ABC为直角三角形,因为AB=8, ![]() ,
,
所以 ![]() ,AC=4,
,AC=4,
在△ACE中,由余弦定理:CE2=AC2+AE2﹣2ACAEcosA,且 ![]() ,
,
所以13=16+AE2﹣4AE,
解得AE=1或AE=3
(2)解:因为 ![]() ,
, ![]() ,
,
所以∠ACE=α ![]() ,
,
所以 ![]() ,
,
在△ACF中由正弦定理得: ![]() ,
,
所以 ![]() ,
,
在△ACE中,由正弦定理得: ![]() ,
,
所以 ![]() ,
,
由于: ![]() ,
,
因为 ![]() ,所以
,所以 ![]() ,所以
,所以 ![]() ,
,
所以当 ![]() 时,S△ECF取最大值为
时,S△ECF取最大值为 ![]()
【解析】(1)由已知利用余弦定理,即可求AE的长;(2)设∠ACE=α,求出CF,CE,利用三角形面积公式可求S△CEF , 求出最大值,即可求该空地产生最大经济价值时种植甲种水果的面积.
【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识,掌握正弦定理:![]() ,以及对余弦定理的定义的理解,了解余弦定理:
,以及对余弦定理的定义的理解,了解余弦定理:![]() ;
;![]() ;
;![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】下表是某厂的产量x与成本y的一组数据:
产量x(千件) | 2 | 3 | 5 | 6 |
成本y(万元) | 7 | 8 | 9 | 12 |
(Ⅰ)根据表中数据,求出回归直线的方程 ![]() =
= ![]() x
x ![]() (其中
(其中 ![]() =
= 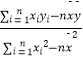 ,
, ![]() =
= ![]() ﹣
﹣ ![]() )
)
(Ⅱ)预计产量为8千件时的成本.