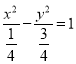题目内容
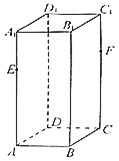
【题目】若长方体![]() 的底面是边长为2的正方形,高为4,
的底面是边长为2的正方形,高为4,![]() 是
是![]() 的中点,则( )
的中点,则( )

A.![]() B.平面
B.平面![]() 平面
平面![]()
C.三棱锥![]() 的体积为
的体积为![]() D.三棱锥
D.三棱锥![]() 的外接球的表面积为
的外接球的表面积为![]()
【答案】CD
【解析】
以![]() 为正交基底建立空间直角坐标系,写出各点坐标,计算
为正交基底建立空间直角坐标系,写出各点坐标,计算![]() 值即可判断A;分别求出平面
值即可判断A;分别求出平面![]() ,平面
,平面![]() 的法向量,判断它们的法向量是否共线,即可判断B;利用等体积法,求出三棱锥
的法向量,判断它们的法向量是否共线,即可判断B;利用等体积法,求出三棱锥![]() 的体积即可判断C;三棱锥
的体积即可判断C;三棱锥![]() 的外接球即为长方体
的外接球即为长方体![]() 的外接球,故求出长方体
的外接球,故求出长方体![]() 的外接球的表面积即可判断D.
的外接球的表面积即可判断D.

以![]() 为正交基底建立如图所示的空间直角坐标系,则
为正交基底建立如图所示的空间直角坐标系,则
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() 与
与![]() 不垂直,故A错误;
不垂直,故A错误;
![]() ,
,![]()
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则
由 ,得
,得 ,所以
,所以 ,
,
不妨取![]() ,则
,则![]() ,
,![]()
所以![]() ,
,
同理可得设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
故不存在实数![]() 使得
使得![]() ,故平面
,故平面![]() 与平面
与平面![]() 不平行,故B错误;
不平行,故B错误;
在长方体![]() 中,
中,![]() 平面
平面![]() ,
,
故![]() 是三棱锥
是三棱锥![]() 的高,
的高,
所以![]() ,
,
故C正确;
三棱锥![]() 的外接球即为长方体
的外接球即为长方体![]() 的外接球,
的外接球,
故外接球的半径![]() ,
,
所以三棱锥![]() 的外接球的表面积
的外接球的表面积![]() ,故D正确.
,故D正确.
故选:CD.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
【题目】总体由编号为01,02,…,19,20的20个个体组成,利用下面的随机数表选取6个个体,选取方法从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的第6个个体的编号为( )
7816 6572 0802 6314 0702 4369 9728 0198 |
3204 9234 4935 8200 3623 4869 6938 7481 |
A.07B.04C.02D.01