题目内容
已知函数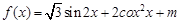 ,其定义域为
,其定义域为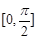 ,最大值为6.
,最大值为6.
(1)求常数m的值;
(2)求函数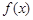 的单调递增区间.
的单调递增区间.
(1)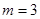 ;(2)
;(2)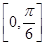
解析试题分析:(1) 首先将函数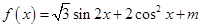 化成
化成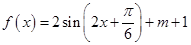
再根据其定义域求出最大值,列方程求出常数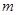 的值.
的值.
(2)根据正弦函数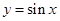 的单调性和
的单调性和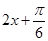 的取值范围,列不等式
的取值范围,列不等式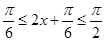 ,可得函数的单调区间.
,可得函数的单调区间.
试题解析:(1)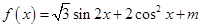
=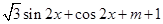
=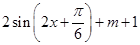
由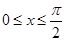 知:
知: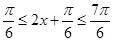 ,于是可知
,于是可知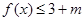
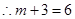 得
得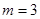 . (6分)
. (6分)
(2)由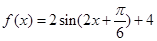 及
及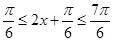
而 在
在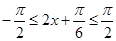 上单调递增
上单调递增
可知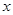 满足:
满足: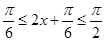 时
时 单调递增
单调递增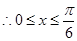
于是 在定义域
在定义域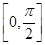 上的单调递增区间为
上的单调递增区间为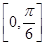 . (12分)
. (12分)
考点:1、正弦函数的性质;2、两角和与差的三角函数公式.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
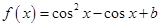 ,
, .
.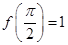 ,求函数
,求函数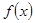 的解析式;
的解析式;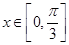 时,
时, 的图像与
的图像与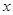 轴有交点,求实数
轴有交点,求实数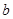 的取值范围.
的取值范围.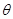 的终边过点P
的终边过点P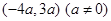 ,
,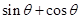 的值
的值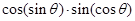 的符号
的符号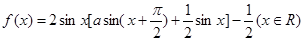 ,的图象关于直线
,的图象关于直线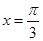 对称,求
对称,求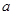 值.
值.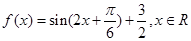 .
. 的最小正周期和单调增区间.
的最小正周期和单调增区间.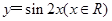 的图象经过怎样的变换得到?
的图象经过怎样的变换得到? ,设函数
,设函数 .
. ]上的最大值和最小值.
]上的最大值和最小值.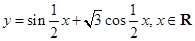 .
. .
. 的最大值,并写出
的最大值,并写出 的取值集合;
的取值集合; 中,角
中,角 的对边分别为
的对边分别为 若
若
 求实数
求实数 的最小值.
的最小值.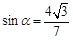 ,
,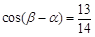 ,且
,且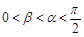 .
.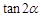 的值;
的值;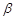 的值.
的值.