题目内容
已知函数
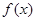 是定义在R上的奇函数,
是定义在R上的奇函数,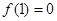 ,
,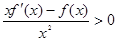
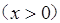 ,
,则不等式
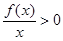 的解集是 .
的解集是 . 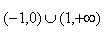
分析:先根据 [
 ]′=
]′= 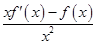 >0判断函数
>0判断函数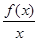 的单调性,进而分别看x>1和0<x<1时f(x)与0的关系.再根据函数的奇偶性判断-1<x<0和x<-1时f(x)与0的关系,最后去x的并集即可得到答案.
的单调性,进而分别看x>1和0<x<1时f(x)与0的关系.再根据函数的奇偶性判断-1<x<0和x<-1时f(x)与0的关系,最后去x的并集即可得到答案.解:[
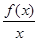 ]′=
]′=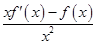 >0,即x>0时
>0,即x>0时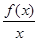 是增函数
是增函数当x>1时,
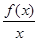 >f(1)=0,f(x)>0;
>f(1)=0,f(x)>0;0<x<1时,
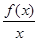 <f(1)=0,f(x)<0.
<f(1)=0,f(x)<0.又f(x)是奇函数,所以-1<x<0时,f(x)=-f(-x)>0;x<-1时f(x)=-f(-x)<0.
则不等式f(x)>0的解集是(-1,0)∪(1,+∞)
故答案为:(-1,0)∪(1,+∞).

练习册系列答案
相关题目
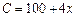 ,月最高产量为150台,出厂单价p(单位:万元)与月产量x的函数关系为
,月最高产量为150台,出厂单价p(单位:万元)与月产量x的函数关系为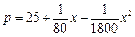 .
.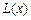 ;
;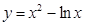 上的一个动点,则点P到直线
上的一个动点,则点P到直线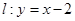 的距离的最小值为( )
的距离的最小值为( )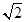
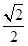
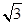
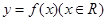 上任一点
上任一点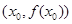 处的切线斜率
处的切线斜率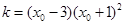 ,则该函数的单调递减区间为
,则该函数的单调递减区间为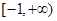
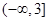
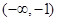
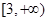
 的单调递减区间是 .
的单调递减区间是 .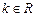 ,函数
,函数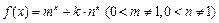 .
.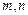 满足
满足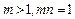 ,函数
,函数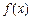 是否具有奇偶性?如果有,求出相应的
是否具有奇偶性?如果有,求出相应的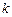
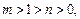 判断函数
判断函数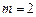 ,
,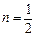 ,且
,且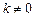 ,求函数
,求函数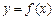 的对称轴或对称中心.
的对称轴或对称中心.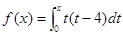 在
在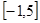 上( )
上( )
 的单调性;
的单调性; 的最大值和最小值.
的最大值和最小值.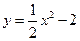 在点
在点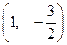 处切线的倾斜角为 ( )
处切线的倾斜角为 ( )