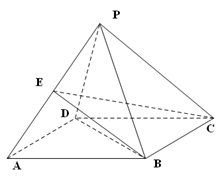
题目内容
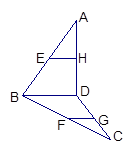
AB为圆O的直径,点E、F在圆上,AB//EF,矩形ABCD所在平面与圆O所在平面互相垂直,已知AB=2,BC=EF=1。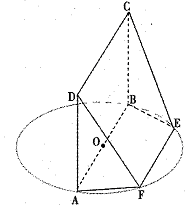
(I)求证:BF⊥平面DAF;
(II)求多面体ABCDFE的体积。
(I)先证AD⊥B,AF⊥BF (II)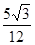
解析试题分析:
(I)证明:因为平面ABCD⊥平面ABEF,AD⊥AB,
∴AD⊥平面ABEF,∴AD⊥BF;
又∵AB为圆O的直径,∴AF⊥BF,
AF∩AD=A,∴BF⊥平面DAF;
(II)作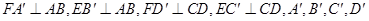 为垂足,则
为垂足,则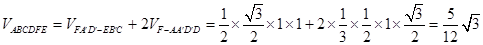
考点:直线与平面垂直的判定体积求法
点评:本题考查的知识点是直线与平面所成的角,直线与平面平行的判定,直线与平面垂直的判定,其中(1)的关键是得到BF⊥AF,DA⊥BF.

练习册系列答案
相关题目
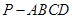 的底面
的底面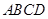 是边长为2的菱形,
是边长为2的菱形,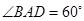 .已知
.已知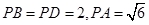 .
.
 为
为 的中点,求三菱锥
的中点,求三菱锥 的体积.
的体积.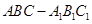 中,
中,

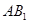 与
与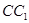 所成角的大小;
所成角的大小;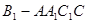 的体积。
的体积。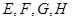 为空间四边形
为空间四边形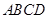 的边
的边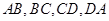 上的点,且
上的点,且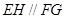 ,求证:
,求证: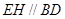 .
.
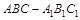 中,
中,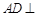 平面
平面 ,其垂足
,其垂足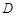 落在直线
落在直线 上.
上.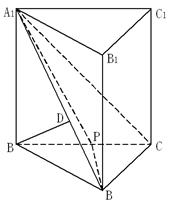
 ;
;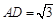 ,
,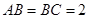 ,
,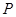 为
为 的中点,求三棱锥
的中点,求三棱锥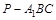 的体积.
的体积.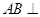 平面
平面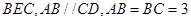 ,
, 为等边三角形.
为等边三角形.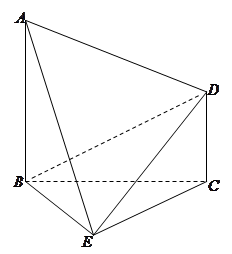
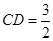 ,求证:平面
,求证:平面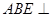 平面
平面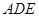 ;
;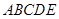 的体积为
的体积为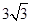 ,求此时二面角
,求此时二面角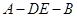 的余弦值.
的余弦值.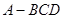 中,
中, 是
是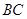 的中点,
的中点, ,
, ,
,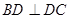 ,
,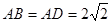 ,二面角
,二面角 的大小为
的大小为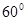 .
.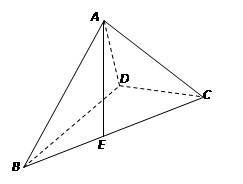
 平面
平面 ;
;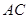 与平面
与平面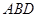 所成角的正弦值.
所成角的正弦值. 和矩形
和矩形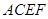 所在的平面互相垂直,
所在的平面互相垂直,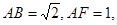
 是线段
是线段 的中点。
的中点。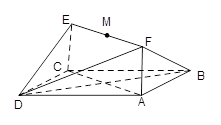
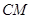 ∥平面
∥平面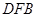
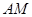 与
与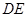 所成的角的余弦值。
所成的角的余弦值。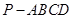 中,底面
中,底面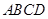 是矩形,侧棱
是矩形,侧棱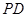 ⊥底面
⊥底面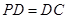 ,
, 是
是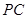 的中点,
的中点,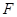 为
为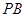 的中点.
的中点.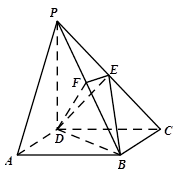
 平面
平面
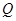 为直线
为直线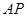 上任意一点,求几何体
上任意一点,求几何体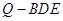 的体积;
的体积;