题目内容
(本小题满分12分)已知函数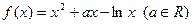
(Ⅰ)若函数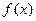 在
在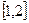 上是减函数,求实数
上是减函数,求实数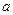 的取值范围;
的取值范围;
(Ⅱ)令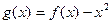 ,是否存在实数
,是否存在实数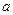 ,使得当
,使得当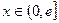 时,函数
时,函数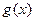 的最小值是
的最小值是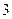 ?若存在,求出实数
?若存在,求出实数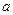 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(Ⅲ)当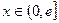 时,证明
时,证明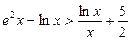 .
.
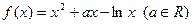
(Ⅰ)若函数
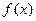 在
在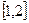 上是减函数,求实数
上是减函数,求实数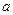 的取值范围;
的取值范围;(Ⅱ)令
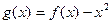 ,是否存在实数
,是否存在实数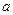 ,使得当
,使得当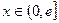 时,函数
时,函数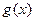 的最小值是
的最小值是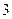 ?若存在,求出实数
?若存在,求出实数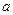 的值;若不存在,说明理由.
的值;若不存在,说明理由.(Ⅲ)当
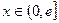 时,证明
时,证明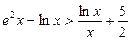 .
.(1)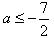 (2)
(2) (3)略
(3)略
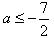 (2)
(2) (3)略
(3)略(I)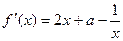 …………………………………1分
…………………………………1分
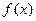 在
在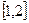 上单调递减,因此当
上单调递减,因此当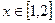 时,
时, 恒成立
恒成立
即 ,化简得
,化简得 (
(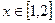 )
)
令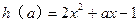 ,即
,即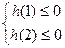 ,
, ………………………………4分
………………………………4分
(II) ,
, …………………………………5分
…………………………………5分
当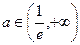 时
时
 ,
,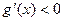 ,
,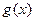 单调递减;
单调递减;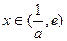 ,
,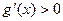 ,
,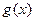 单调递增;
单调递增;
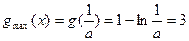 ,
,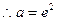
当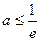 时,
时,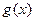 单调递减,
单调递减, ,
,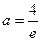 (舍)
(舍)
综上 ………………………………8分
………………………………8分
(III)由(II)可知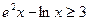
令 ,
, , …………………………………9分
, …………………………………9分
当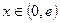 时,
时,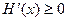 ,
, 单调递增,
单调递增,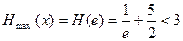
即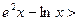
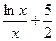 恒成立 …………………………………12分
恒成立 …………………………………12分
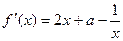 …………………………………1分
…………………………………1分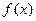 在
在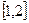 上单调递减,因此当
上单调递减,因此当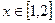 时,
时, 恒成立
恒成立即
 ,化简得
,化简得 (
(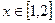 )
)令
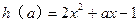 ,即
,即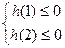 ,
, ………………………………4分
………………………………4分(II)
 ,
, …………………………………5分
…………………………………5分当
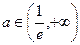 时
时 ,
,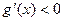 ,
,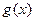 单调递减;
单调递减;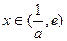 ,
,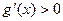 ,
,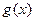 单调递增;
单调递增;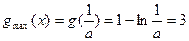 ,
,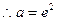
当
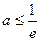 时,
时,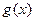 单调递减,
单调递减, ,
,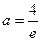 (舍)
(舍)综上
 ………………………………8分
………………………………8分(III)由(II)可知
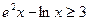
令
 ,
, , …………………………………9分
, …………………………………9分当
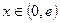 时,
时,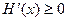 ,
, 单调递增,
单调递增,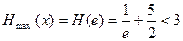
即
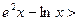
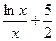 恒成立 …………………………………12分
恒成立 …………………………………12分
练习册系列答案
相关题目
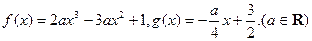
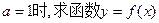 的单调区间;
的单调区间;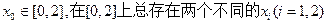 ,使得
,使得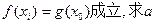 的取值范围.
的取值范围.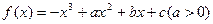 ,在
,在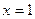 处取得极大值,且存在斜率为
处取得极大值,且存在斜率为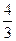 的切线。
的切线。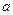 的取值范围;
的取值范围;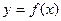 在区间
在区间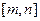 上单调递增,求
上单调递增,求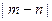 的取值范围;
的取值范围;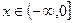 ,都有
,都有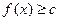 。
。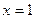 是函数
是函数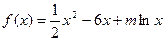 的一个极值点。
的一个极值点。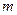 ;
;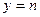 与函数
与函数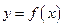 的图象有3个交点,求
的图象有3个交点,求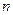 的取值范围;
的取值范围;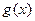 =(
=(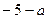 )
)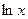 +
+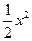 +(6-
+(6-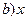 +2(
+2(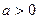 ),
),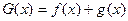 ,若
,若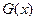 =0有两个零点
=0有两个零点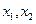 ,且
,且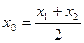 ,试探究
,试探究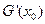 值的符号
值的符号
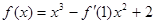 ,则
,则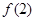 为
为



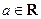 ,函数
,函数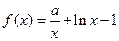 ,
,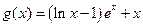 (其中
(其中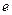 为自然对数的底数).
为自然对数的底数).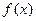 在区间
在区间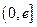 上的最小值;
上的最小值;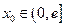 ,使曲线
,使曲线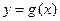 在点
在点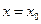 处的切线与
处的切线与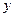 轴垂直? 若存在,求出
轴垂直? 若存在,求出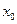 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.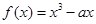 (
(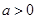 )的零点都在区间[-10,10]上,则使得方程
)的零点都在区间[-10,10]上,则使得方程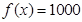 有正整数解的实数
有正整数解的实数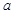 的取值个数为 ( )
的取值个数为 ( )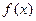 是R上可导的偶函数,
是R上可导的偶函数,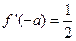 ,则
,则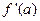 的值为( ).
的值为( ).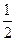
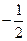
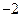
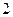
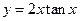 的导数是( )
的导数是( )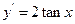 B
B 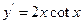 C
C 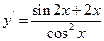 D
D