题目内容
叙述并证明余弦定理.
见解析
本题是课本公式、定理、性质的推导,这是高考考查的常规方向和考点,引导考生回归课本,重视基础知识学习和巩固.
叙述:
余弦定理:三角形任何一边的平方等于其他两遍平方的和减去这两边与它们夹角的余弦之积的两倍。或:在△ABC中,a,b,c为A,B,C的对边,有
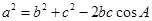 ,
,
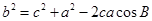 ,
,
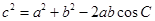 .
.

证明:(证法一) 如图,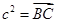
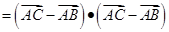
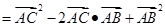
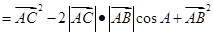
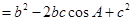
即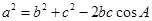
同理可证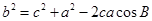 ,
,
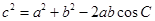
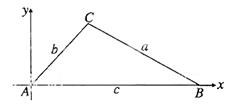
(证法二)已知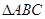 中,
中,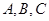 所对边分别为
所对边分别为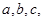 ,以
,以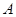 为原点,
为原点,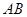 所在直线为
所在直线为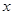 轴建立直角坐标系,则
轴建立直角坐标系,则 ,
,
∴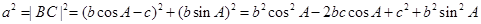
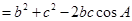 ,
,
即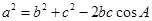
同理可证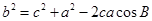 ,
,
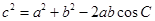
叙述:
余弦定理:三角形任何一边的平方等于其他两遍平方的和减去这两边与它们夹角的余弦之积的两倍。或:在△ABC中,a,b,c为A,B,C的对边,有
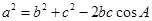 ,
,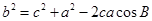 ,
,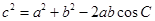 .
.
证明:(证法一) 如图,
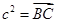
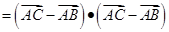
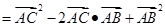
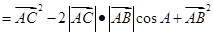
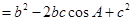
即
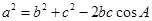
同理可证
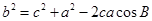 ,
,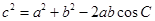
(证法二)已知
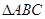 中,
中,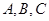 所对边分别为
所对边分别为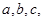 ,以
,以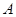 为原点,
为原点,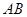 所在直线为
所在直线为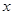 轴建立直角坐标系,则
轴建立直角坐标系,则 ,
,∴
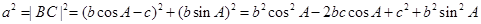
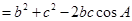 ,
,
即
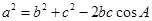
同理可证
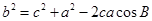 ,
,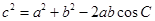

练习册系列答案
相关题目
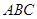 中,
中,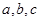 是角
是角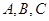 对应的边,向量
对应的边,向量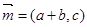 ,
,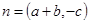 ,且
,且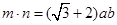 .
.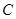 ;
;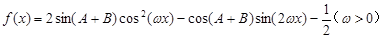 的相邻两个极值的横坐标分别为
的相邻两个极值的横坐标分别为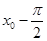 、
、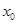 ,求
,求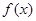 的单调递减区间.
的单调递减区间.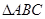 中,
中,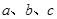 分别为内角
分别为内角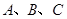 的对边,且
的对边,且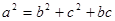
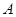 的大小;
的大小;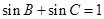 ,试求内角B、C的大小.
,试求内角B、C的大小.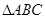 的内角
的内角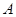 、
、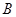 、
、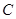 的对边分别为
的对边分别为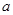 、
、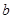 、
、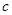 ,且
,且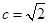 ,
,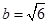 ,
,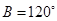 ,则
,则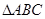 中,
中,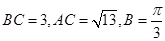 ,则
,则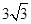

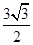
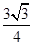
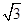 bc,则角B=________.
bc,则角B=________.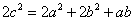 ,则△ABC是( )
,则△ABC是( )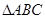 中,
中,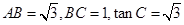 ,则
,则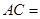 ______.
______.