题目内容
空间四边形OABC,各边及对角线长都相等,E、F分别为AB、OC的中点,求OE与BF所成的角。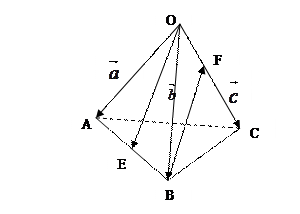

抛物线的方程为y2=4x
如图,设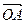 =
=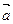 ,
,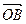 =
= ,
,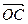 =
=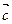 ,且|
,且|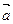 |=|
|=| |=|
|=|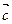 |=1,易知∠AOB=∠BOC=∠AOC=
|=1,易知∠AOB=∠BOC=∠AOC=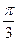 ,则
,则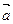 ·
· =
= ·
·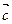 =
=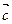 ·
·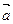 =
=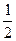 。
。
∵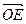 =
=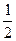 (
(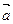 +
+ ),
),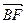 =
=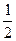
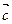 -
- ,|
,|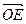 |=|
|=|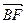 |=
|=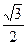 ,
,
∴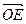 ·
·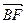 =
=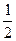 (
(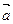 +
+ )·(
)·(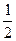
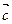 -
- )=
)=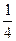
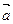 ·
·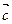 +
+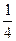
 ·
·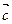 -
-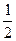
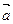 ·
· -
-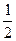 |
| |
|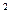 =-
=-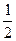 ,∴COS<
,∴COS<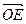 ,
,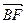 >=
>=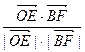 =-
=-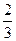 ,
,
∴<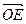 ,
,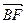 >=
>=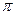 -arccos
-arccos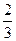 。
。
因此,异面直线OE与BF所成的角为arccos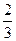
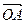 =
=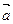 ,
,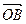 =
= ,
,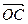 =
=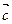 ,且|
,且|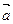 |=|
|=| |=|
|=|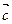 |=1,易知∠AOB=∠BOC=∠AOC=
|=1,易知∠AOB=∠BOC=∠AOC=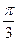 ,则
,则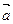 ·
· =
= ·
·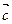 =
=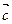 ·
·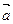 =
=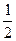 。
。∵
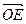 =
=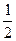 (
(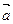 +
+ ),
),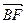 =
=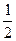
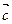 -
- ,|
,|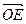 |=|
|=|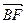 |=
|=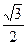 ,
,∴
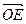 ·
·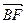 =
=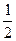 (
(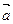 +
+ )·(
)·(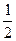
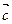 -
- )=
)=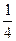
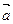 ·
·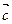 +
+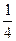
 ·
·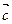 -
-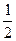
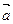 ·
· -
-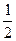 |
| |
|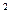 =-
=-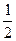 ,∴COS<
,∴COS<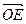 ,
,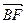 >=
>=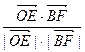 =-
=-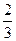 ,
,∴<
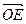 ,
,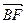 >=
>=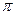 -arccos
-arccos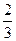 。
。因此,异面直线OE与BF所成的角为arccos
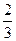

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
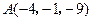 ,
,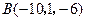 ,
,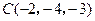 为顶点的三角形是等腰直角三角形.
为顶点的三角形是等腰直角三角形.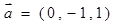 ,
,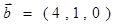 ,
, 且
且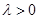 ,则
,则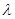 = ____________.
= ____________.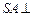 面
面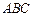 ,
,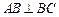 ,
,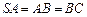 ,求异面直线
,求异面直线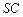 与
与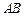 所成角的余弦值.
所成角的余弦值.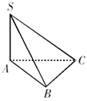
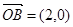 ,向量
,向量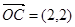 ,向量
,向量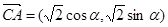 ,则向量
,则向量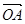 与向量
与向量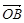 的夹角的取值范围是( )
的夹角的取值范围是( )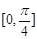
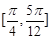
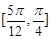
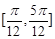
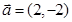 ,则与
,则与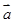 垂直的单位向量的坐标为__________
垂直的单位向量的坐标为__________ 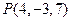 关于平面
关于平面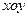 的对称点的坐标为
的对称点的坐标为 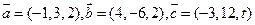 ,若
,若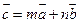 ,
,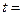 .
.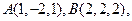 点
点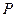 在
在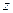 轴上,且
轴上,且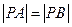 ,则点
,则点