题目内容
设a∈R,f(x)为奇函数,且f(2x)=| a•4x-a-2 |
| 4x+1 |
(1)试求f(x)的反函数f-1(x)的解析式及f-1(x)的定义域;
(2)设g(x)=log
| 2 |
| 1+x |
| k |
| 1 |
| 2 |
| 2 |
| 3 |
分析:(1)利用f(x)为奇函数当x=0有意义,则f(0)=0,求出a,求出f(x)的解析式;将函数f(x)看出关于x的方程,求出x,将x换成y,将y换成x求出反函数,求出f(x)的值域即反函数的定义域.
(2)先利用对数函数的真数大于0求出k的范围;利用对数函数的单调性去掉对数符号,将不等式转化为二次不等式恒成立;转化为函数的求最值.
(2)先利用对数函数的真数大于0求出k的范围;利用对数函数的单调性去掉对数符号,将不等式转化为二次不等式恒成立;转化为函数的求最值.
解答:解:(1)因为f(x)为奇函数,且x∈R所以f(0)=0,得a=1,f(x)=
f-1(x)=log2
,x∈(-1,1)(6分)
(2)假设存在满足条件的实数k.
因为x∈[
,
],所以k>0
由f-1(x)≤g(x)得log2
≤log
,所以0<
≤(
)2,
所以当x∈[
,
]时,k2≤1-x2恒成立(10分)
即k2≤(1-x2)min=
,又k>0
所以k的取值范围是0<k≤
(14分)
| 2x-1 |
| 2x+1 |
| 1+x |
| 1-x |
(2)假设存在满足条件的实数k.
因为x∈[
| 1 |
| 2 |
| 2 |
| 3 |
由f-1(x)≤g(x)得log2
| 1+x |
| 1-x |
| 2 |
| 1+x |
| k |
| 1+x |
| 1-x |
| 1+x |
| k |
所以当x∈[
| 1 |
| 2 |
| 2 |
| 3 |
即k2≤(1-x2)min=
| 5 |
| 9 |
所以k的取值范围是0<k≤
| ||
| 3 |
点评:本题考查奇函数的特殊函数值f(0)=0、考查反函数的求法、利用对数函数的单调性解决对数不等式问题,解决不等式恒成立常转化为函数的最值.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
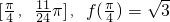 .给出下列几个命题:
.给出下列几个命题: 处取得小值;
处取得小值;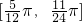 是f(x)的一个单调递减区间;
是f(x)的一个单调递减区间; .
.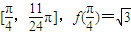 .给出下列几个命题:
.给出下列几个命题: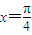 处取得小值;
处取得小值;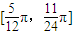 是f(x)的一个单调递减区间;
是f(x)的一个单调递减区间;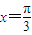 .
.