题目内容
给出下列命题:
①如果向量 ,
, ,
, 共面,向量
共面,向量 ,
, ,
, 也共面,则向量
也共面,则向量 ,
, ,
, ,
, 共面;
共面;
②已知直线a的方向向量 与平面α,若
与平面α,若 ∥平面α,则直线a∥平面α;
∥平面α,则直线a∥平面α;
③若P、M、A、B共面,则存在唯一实数x、y使 =x
=x +y
+y ;
;
④对空间任意点O与不共线的三点A、B、C,若 =x
=x +y
+y +z
+z (其中x+y+z=1),则P、A、B、C四点共面; 在这四个命题中为真命题的序号有________.
(其中x+y+z=1),则P、A、B、C四点共面; 在这四个命题中为真命题的序号有________.
④
分析:我们可以根据共面向量的性质对四个结论逐一进行判断,
①令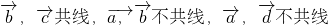 ,则满足,但
,则满足,但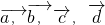 不一定共面,①不对,
不一定共面,①不对,
②若 ∥平面α,则直线a∥平面α或a?α,所以②也不对;
∥平面α,则直线a∥平面α或a?α,所以②也不对;
③不妨令M、A、B三点共线,点P∉AB,则不存在实数x、y满足条件式,③错;
④由共面向量基本定理的推论,可得④正确.
解答:①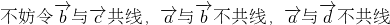 ,满足向量
,满足向量 ,
, ,
, 共面,向量
共面,向量 ,
, ,
, 也共面,但向量
也共面,但向量 ,
, ,
, ,
, 不一定共面,故①不正确;
不一定共面,故①不正确;
②若 ∥平面α,则直线a∥平面α或a?α,故②不正确;
∥平面α,则直线a∥平面α或a?α,故②不正确;
③不妨令M、A、B三点共线,点P∉AB,则不存在实数x、y使 =x
=x +y
+y ,故③不正确;
,故③不正确;
④∵三点A、B、C不共线, =x
=x +y
+y +z
+z ,x+y+z=1,
,x+y+z=1,
∴ =x
=x +y
+y +(1-x-y)
+(1-x-y) =
=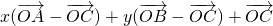 =
=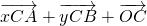 ,∴
,∴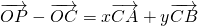
 ,由共面向量基本定理知,P、A、B、C四点共面,故④正确.
,由共面向量基本定理知,P、A、B、C四点共面,故④正确.
故答案为:④
点评:本题考查空间向量中的概念,共面向量基本定理及推论,解决的主要方法是特例法与转化思想的灵活运用.
分析:我们可以根据共面向量的性质对四个结论逐一进行判断,
①令
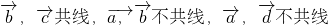 ,则满足,但
,则满足,但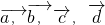 不一定共面,①不对,
不一定共面,①不对,②若
 ∥平面α,则直线a∥平面α或a?α,所以②也不对;
∥平面α,则直线a∥平面α或a?α,所以②也不对;③不妨令M、A、B三点共线,点P∉AB,则不存在实数x、y满足条件式,③错;
④由共面向量基本定理的推论,可得④正确.
解答:①
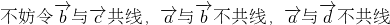 ,满足向量
,满足向量 ,
, ,
, 共面,向量
共面,向量 ,
, ,
, 也共面,但向量
也共面,但向量 ,
, ,
, ,
, 不一定共面,故①不正确;
不一定共面,故①不正确;②若
 ∥平面α,则直线a∥平面α或a?α,故②不正确;
∥平面α,则直线a∥平面α或a?α,故②不正确;③不妨令M、A、B三点共线,点P∉AB,则不存在实数x、y使
 =x
=x +y
+y ,故③不正确;
,故③不正确;④∵三点A、B、C不共线,
 =x
=x +y
+y +z
+z ,x+y+z=1,
,x+y+z=1,∴
 =x
=x +y
+y +(1-x-y)
+(1-x-y) =
=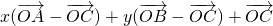 =
=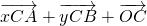 ,∴
,∴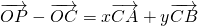
 ,由共面向量基本定理知,P、A、B、C四点共面,故④正确.
,由共面向量基本定理知,P、A、B、C四点共面,故④正确.故答案为:④
点评:本题考查空间向量中的概念,共面向量基本定理及推论,解决的主要方法是特例法与转化思想的灵活运用.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目