题目内容
10.设A为4×3阶矩阵,且r(A)=2,而B=$[\begin{array}{l}{1}&{0}&{2}\\{0}&{2}&{0}\\{-1}&{0}&{3}\end{array}]$,则r(AB)=2.分析 由已知得B为可逆矩阵,即B为满秩矩阵.当一个矩阵与一个满秩矩阵相乘时,所得的矩阵的秩与原矩阵相等.
解答 解:∵B=$[\begin{array}{l}{1}&{0}&{2}\\{0}&{2}&{0}\\{-1}&{0}&{3}\end{array}]$,
∴|B|=$[\begin{array}{l}{1}&{0}&{2}\\{0}&{2}&{0}\\{-1}&{0}&{3}\end{array}]$=6+4=10≠0,
∴B=$[\begin{array}{l}{1}&{0}&{2}\\{0}&{2}&{0}\\{-1}&{0}&{3}\end{array}]$是满秩矩阵,
∵A为4×3阶矩阵,且r(A)=2,
∴r(AB)=2.
点评 本题考查AB的秩的求法,是基础题,解题时要认真审题,解题时要注意矩阵的秩的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.在四棱锥P-ABCD中,PD⊥底面ABCD,四边形ABCD为正方形,且PD=AB=1,$\overrightarrow{BG}$=$\frac{1}{3}$$\overrightarrow{BD}$,则$\overrightarrow{PG}$与底面ABCD的夹角的正弦值为( )
| A. | $\frac{2\sqrt{34}}{17}$ | B. | $\frac{3\sqrt{17}}{17}$ | C. | -$\frac{2\sqrt{34}}{17}$ | D. | -$\frac{3\sqrt{17}}{17}$ |
1.若a=i+i2+…+i2013(i是虚数单位),则$\frac{a(1+a)^{2}}{1-a}$的值为( )
| A. | i | B. | 1-i | C. | -1+i | D. | -1-i |
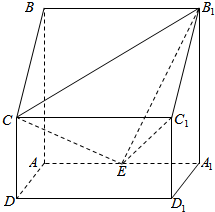 四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥CD,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.
四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥CD,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.