题目内容
20.椭圆若椭圆的对称轴在坐标轴上,两焦点与两短轴端点正好是正方形的四个顶点,又焦点到同侧长轴端点的距离为$\sqrt{2}-1$,求椭圆的方程$\frac{x^2}{2}+{y^2}=1或\frac{y^2}{2}+{x^2}=1$.分析 由题意推出椭圆的关系,b=c,利用焦点到同侧长轴端点距离为$\sqrt{2}-1$,求出a,b,即可求出椭圆的方程.
解答 解:因为椭圆的对称轴在坐标轴,两焦点与两短轴的端点恰好是正方形的四个顶点,
所以b=c,a=$\sqrt{2}$b,又焦点到同侧长轴端点距离为$\sqrt{2}-1$,
即a-c=$\sqrt{2}-1$,即a-b=$\sqrt{2}-1$,解得a=$\sqrt{2}$,b=c=1,
所以当焦点在x轴时,椭圆的方程为:$\frac{{x}^{2}}{2}+{y}^{2}$=1;
当焦点在y轴时,椭圆的方程为$\frac{{y}^{2}}{2}+{x}^{2}$=1.
故答案为:$\frac{x^2}{2}+{y^2}=1或\frac{y^2}{2}+{x^2}=1$.
点评 本题考查椭圆的方程的求法,椭圆的基本性质,考查计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.$\sqrt{5}+1$与$\sqrt{5}-1$两数的等比中项是(
| A. | 2 | B. | -2 | C. | ±2 | D. | 以上均不是 |
12.定义在D上的函数f(x)若同时满足:①存在M>0,使得对任意的x1,x2∈D,都有|f(x1)-f(x2)|<M;②f(x)的图象存在对称中心.则称f(x)为“P-函数”.
已知函数f1(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$和f2(x)=lg($\sqrt{{x}^{2}+1}$-x),则以下结论一定正确的是( )
已知函数f1(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$和f2(x)=lg($\sqrt{{x}^{2}+1}$-x),则以下结论一定正确的是( )
| A. | f1(x)和 f2(x)都是P-函数 | B. | f1(x)是P-函数,f2(x)不是P-函数 | ||
| C. | f1(x)不是P-函数,f2(x)是P-函数 | D. | f1(x)和 f2(x)都不是P-函数 |
9.下列各组函数中,表示同一函数的是( )
| A. | f(x)=2x-1•2x+1,g(x)=4x | B. | $f(x)=\sqrt{x^2},g(x)={({\sqrt{x}})^2}$ | ||
| C. | $f(x)=\frac{{{x^2}-2}}{{x-\sqrt{2}}},g(x)=x+\sqrt{2}$ | D. | $f(x)=\sqrt{x+1}•\sqrt{x-1},g(x)=\sqrt{{x^2}-1}$ |
10.若0<x<y,则下列各式正确的是( )
| A. | x3<y3 | B. | log${\;}_{\frac{1}{3}}$x<log${\;}_{\frac{1}{3}}$y | ||
| C. | ($\frac{1}{3}$)x$<(\frac{1}{3})^{y}$ | D. | $\frac{3}{x}<\frac{3}{y}$ |
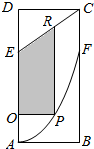 某市政府欲在如图所示的矩形ABCD的非农业用地中规划出一个休闲娱乐公园(如图中阴影部分),形状为直角梯形OPRE(线段EO和RP为两条底边),已知AB=2km,BC=6km,AE=BF=4km,其中曲线AF是以A为顶点、AD为对称轴的抛物线的一部分.
某市政府欲在如图所示的矩形ABCD的非农业用地中规划出一个休闲娱乐公园(如图中阴影部分),形状为直角梯形OPRE(线段EO和RP为两条底边),已知AB=2km,BC=6km,AE=BF=4km,其中曲线AF是以A为顶点、AD为对称轴的抛物线的一部分.