题目内容
5.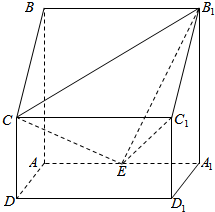 四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥CD,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.
四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥CD,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.(1)求证:B1C1⊥CE
(2)求点C到平面B1C1E的距离.
分析 (1)以点A为原点,AD为x轴,建立空间直角坐标系,利用向量法能证明B1C1⊥CE.
(2)求出平面B1C1E的法向量,利用向量法能求出点C到平面B1C1E的距离.
解答 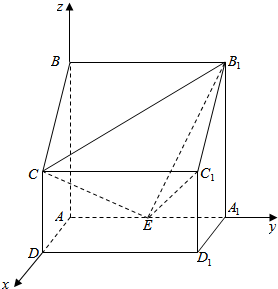 (1)证明:以点A为原点,AD为x轴,建立空间直角坐标系,
(1)证明:以点A为原点,AD为x轴,建立空间直角坐标系,
则B1(0,2,2),C1(1,2,1),C(1,0,1),E(0,1,0),
$\overrightarrow{{B}_{1}{C}_{1}}$=(1,0,-1),$\overrightarrow{CE}$=(-1,1,-1),
∴$\overrightarrow{{B}_{1}{C}_{1}}$•$\overrightarrow{CE}$=0,∴B1C1⊥CE.
(2)解:设平面B1C1E的法向量$\overrightarrow{n}$=(x,y,z),
∵$\overrightarrow{{B}_{1}{C}_{1}}$=(1,0,-1),$\overrightarrow{{B}_{1}E}$=(0,-1,-2)
∴$\left\{\begin{array}{l}{x-z=0}\\{-y-2z=0}\end{array}\right.$,
∴取$\overrightarrow{n}$=(1,-2,1),
∵$\overrightarrow{CE}$=(-1,1,-1),
∴点C到平面B1C1E的距离为$\frac{|-1-2-1|}{\sqrt{1+4+1}}$=$\frac{2\sqrt{6}}{3}$.
点评 本题考查异面直线垂直的证明,考查点C到平面B1C1E的距离的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
14.直线3x-2y-6=0的横、纵截距之和等于( )
| A. | -1 | B. | 1 | C. | 4 | D. | 5 |
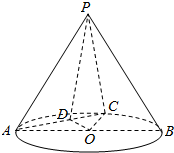 如图,在圆锥PO中,已知PO=$\sqrt{2}$,圆O的直径AB=2,C是弧AB的中点,D为AC的中点.
如图,在圆锥PO中,已知PO=$\sqrt{2}$,圆O的直径AB=2,C是弧AB的中点,D为AC的中点.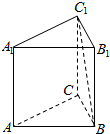 如图,在正三棱柱ABC-A1B1C1中,侧棱长为2$\sqrt{2}$,底面三角形的边长为2,则BC1与侧面ACC1A1所成角的大小为30°.
如图,在正三棱柱ABC-A1B1C1中,侧棱长为2$\sqrt{2}$,底面三角形的边长为2,则BC1与侧面ACC1A1所成角的大小为30°. 如图,G是△OAB的重心,P,Q分别是边OA,OB上的动点(P点可以和A点重合,Q点可以与B点重合),且P,G,Q三点共线.
如图,G是△OAB的重心,P,Q分别是边OA,OB上的动点(P点可以和A点重合,Q点可以与B点重合),且P,G,Q三点共线.