题目内容

19．画出函数y=|-x2+2x+3|的图象，并指出其单调区间．

分析 先把函数y=-x2+2x+3化成顶点式，即可直接得出其顶点坐标，分别令x=0，y=0求出图象与x、y轴的交点，根据其四点可画出函数的图象，根据图象，即可求得函数的单调区间．

解答 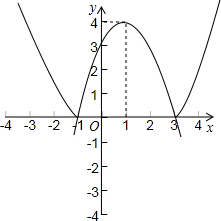解：∵y=-x2+2x+3=-（x-1）2+4，
∴y=-x2+2x+3图象开口方向向下，对称轴x=1，顶点坐标（1，4），
令x=0得：y=3，∴与y轴交点坐标（0，3），
令y=0得：-x2+2x+3=0，∴x1=1 x2=3，
∴与x轴交点坐标（-1，0），（3，0），
作出函数y=-x2+2x+3的图象，并把x轴下方的图象翻折到x轴上方，如图所示
由图象可知，函数的单调减区间为（-∞，-1），（1，3）；单调增区间为（-1，1），（3，+∞）；

点评 本题考查的是二次函数的性质，只要根据题意把函数的一般式化为顶点式，在利用翻折变换画出函数的图象，便可轻松解答．

练习册系列答案
相关题目
5．已知函数f（x）=sin（x+$\frac{π}{6}$）cos（x+$\frac{π}{3}$），求函数g（x）=f（x）+sinx在区间[-$\frac{π}{6}$，$\frac{2π}{3}$]上的值域．
10．判断下列各组中的两个集合间的关系．
（1）P={x|x=2n，n∈Z}，Q={x|x=4n，n∈Z}；
（2）P={x|x=2n-1，n∈N*}，Q={x|x=2n+1，n∈N*}；
（3）P={x|x2-x=0}，Q={x|x=$\frac{1+（-1）^{n}}{2}$，n∈Z}；
（4）已知集合A={x|x=$\frac{1}{9}$（2k+1），k∈Z}，B={x|x=$\frac{4}{9}$k±$\frac{1}{9}$，k∈Z}．
7．在锐角△ABC中，tanA=t+1，tanB=t-1，则实数t的取值范围是（　　）
A．（$\sqrt{2}$，+∞）B．（1，+∞）C．（1，$\sqrt{2}$）D．（-1，1）
14．已知函数f（x）=ex-mx-exlnx+1，且定义域为（0，e]，若函数f（x）在定义域内有两个极值点，则m的取值范围为（　　）
A．[0，ee-2e]B．（0，ee-2e]C．（0，ee-2e）D．（ee-2e，+∞）
4．给出以下四个命题：
①正态曲线当μ一定时曲线形状由σ确定，σ越小曲线越“瘦高”表示总体分布越集中；
②过点（-1，2）且在x轴和y轴上的截距相等的直线方程是x+y-1=0；
③函数f（x）=2x+2x-3在定义域内有且只有一个零点；
④回归方程拟合效果可用R2=1-$\frac{\sum_{i=1}^{n}（{y}_{i}-\stackrel{∧}{{y}_{i}}）^{2}}{\sum_{i=1}^{n}（{y}_{i}-\overline{y}）^{2}}$刻画，R2越接近1表示回归效果越差；
其中正确命题的序号为①③．（把你认为正确的命题序号都填上）
11．已知|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=5，$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{3}$，则|$\overrightarrow{a}$-$\overrightarrow{b}$|等于（　　）
A．5$\sqrt{3}$B．$\frac{5\sqrt{3}}{2}$C．$\sqrt{3}$D．5
8．（2+x+x2）（1-$\frac{1}{x}$）3的展开式中常数项为（　　）
A．-2B．5C．4D．2
9．在△ABC中，角A，B，C所对的边分别为a，b，c，且满足A=60°，sinB+sinC=2sinA，bc=5，则a的值为（　　）
A．2B．$\sqrt{5}$C．3D．4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网