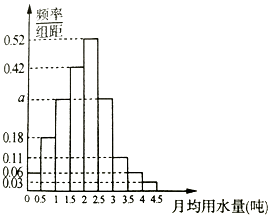
��Ŀ����
����Ŀ��[ѡ��4-4������ϵ���������]����ƽ����ȡ��һ��������ϵ���Լ�����Ϊֱ������ϵ��x��������ᣬ�Ԧ�= ![]() ��������Ϊy��������ᣬ�Լ���Ϊ����ԭ�㣬���ȵ�λ���䣬����ֱ������ϵ����֪����C��ֱ�����귽��Ϊx2+y2=2��ֱ��l�IJ�������
��������Ϊy��������ᣬ�Լ���Ϊ����ԭ�㣬���ȵ�λ���䣬����ֱ������ϵ����֪����C��ֱ�����귽��Ϊx2+y2=2��ֱ��l�IJ������� ![]() ��tΪ��������
��t��������
��1��д��ֱ��l����ͨ����������C�ļ����귽�̣�
��2����ƽ���������任���������ʽΪ ![]() ����C�ڴ˱任�µõ�����C'�ķ��̣���������C���ڽӾ��ε���������
����C�ڴ˱任�µõ�����C'�ķ��̣���������C���ڽӾ��ε���������
���𰸡�
��1���⣺��ֱ��l�IJ������� ![]() ��tΪ����������ȥ��������Ϊֱ�����귽��Ϊ 2x+y��2=0��
��tΪ����������ȥ��������Ϊֱ�����귽��Ϊ 2x+y��2=0��
����C��ֱ�����귽��Ϊx2+y2=2���� ��2=2���� ��= ![]() ��
��
��2���⣺��ƽ���������任���������ʽΪ ![]() ��
��
����C�ڴ˱任�µõ�����C'�ķ���Ϊ ![]() +Y2=2����
+Y2=2���� ![]() +
+ ![]() =1��
=1��
����C'�IJ�������Ϊ 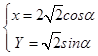 ��������Բ�ĶԳ��ԣ����ߵ��ڽӾ��ε����Ϊ4|XY|=8|sin2��|��
��������Բ�ĶԳ��ԣ����ߵ��ڽӾ��ε����Ϊ4|XY|=8|sin2��|��
�ʵ���= ![]() ʱ�����ߵ��ڽӾ��ε�������Ϊ8��
ʱ�����ߵ��ڽӾ��ε�������Ϊ8��
����������1����ֱ��l�IJ���������ȥ��������Ϊֱ�����귽�̣�����C��ֱ�����귽��Ϊx2+y2=2������2=2������ɵý������2�����������C�ڴ˱任�µõ�����C'�ķ���Ϊ ![]() +Y2=2�����������C'�IJ�������Ϊ
+Y2=2�����������C'�IJ�������Ϊ ![]() ��������Բ�ĶԳ��ԣ����ߵ��ڽӾ��ε����Ϊ4|XY|=8|sin2��|���ɴ˿ɵ����ߵ��ڽӾ��ε�������ֵ��
��������Բ�ĶԳ��ԣ����ߵ��ڽӾ��ε����Ϊ4|XY|=8|sin2��|���ɴ˿ɵ����ߵ��ڽӾ��ε�������ֵ��