��Ŀ����
����Ŀ���ҹ�������������ȱˮ�Ĺ��ң�ij������Ϊ�˹��������Լ��ˮ���ƻ���������������ˮ�շѷ�������ȷ��һ������������ˮ����x���֣���һλ���������ˮ��������x�IJ��ְ�ƽ���շѣ�����x�IJ��ְ�����շѣ�Ϊ���˽������ˮ�����ͨ�������������ij��100λ����ÿ�˵��¾���ˮ������λ���֣��������ݰ���[0��0.5����[0.5��1��������[4��4.5���ֳ�9�飬�Ƴ�����ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��
������ֱ��ͼ��a��ֵ��
��������Ƶ����Ϊ���ʣ��Ӹó��о����������ȡ3�ˣ�����3�����¾���ˮ��������3�ֵ�����ΪX����X�ķֲ�������ѧ������
��������������ϣ��ʹ85%�ľ���ÿ�µ���ˮ����������x���֣�������x��ֵ����ȷ��0.01������˵�����ɣ�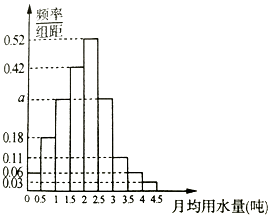
���𰸡����⣺����Ƶ�ʺ�Ϊ1����
��0.06+0.18+2a+0.42+0.52+0.11+0.06+0.03����0.5=1��
���a=0.30��
�⣺�¾���ˮ��������3�ֵ�Ƶ��Ϊ
��0.11+0.06+0.03����0.5=0.1��
��p=0.1����ȡ������ΪX��
��X�Ŀ���ȡֵΪ0��1��2��3��
��P��X=0��= ![]() 0.93=0.729��
0.93=0.729��
P��X=1��= ![]() 0.10.92=0.243��
0.10.92=0.243��
P��X=2��= ![]() 0.120.9=0.027��
0.120.9=0.027��
P��X=3��= ![]() 0.13=0.001��
0.13=0.001��
��X�ķֲ���Ϊ
X | 0 | 1 | 2 | 3 |
P | 0.729 | 0.243 | 0.027 | 0.001 |
������ѧ����ΪEX=0��0.729+1��0.243+2��0.027+3��0.001=0.3��
���⣺��ͼ��֪���¾���ˮ��С��2.5�ֵľ���������ռ�İٷֱ�Ϊ
0.5����0.06+0.18+0.3+0.42+0.52��=0.73��
��73%�ľ����¾���ˮ��С��2.5�֣�
ͬ����88%�ľ����¾���ˮ��С��3�֣�
��2.5��x��3��
�����¾���ˮ��ƽ���ֲ�����
x=2.5+0.5�� ![]() =2.9���֣���
=2.9���֣���
��85%�ľ���ÿ����ˮ����������Ϊ2.9�֣�
��������������Ƶ�ʺ�Ϊ1���г��������a��ֵ���������¾���ˮ��������3�ֵ�Ƶ��ֵ���ɳ�ȡ������X�Ŀ���ȡֵΪ0��1��2��3��
�����Ӧ�ĸ���ֵ��д��X�ķֲ��У�������ѧ����ֵ���������¾���ˮ��С��2.5�ֺ�С��3�ֵİٷֱȣ�
�����85%�ľ�������ˮ���������ı�ֵ��
�����㾫��������Ƶ�ʷֲ�ֱ��ͼ����ɢ�������������ֲ����ǽ����ĸ�������Ҫ֪��Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ���Ƕ���ͬ���ݵ����ֲ�ͬ���﷽ʽ.�ý��յı���ı����ݵ����з�ʽ������ʽ����չʾ���ݵķֲ����.ͨ����ͼ�ȿ��Դ���������ȡ��Ϣ���ֿ�������ͼ�δ�����Ϣ�����������Ʒ����������У������������X����ȡ��ֵ�����ǿ���һ������һһ�г����������������������ɢ�������������ɢ����������ķֲ��У�һ���,����ɢ���������X����ȡ��ֵΪx1,x2,.....,xi,......,xn��Xȡÿһ��ֵ xi(i=1,2,......���ĸ���P(��=xi����Pi����Ʊ�Ϊ��ɢ���������X �ĸ��ʷֲ�����Ʒֲ��У�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��2016������ɫ��������200ǿ���ʳ�¯��������ɽ�����ڵ�28���й�������ѡ�������Ļ�ɽ�羰�����ľ���ӭ���ڶ���ͣ����ںܶ���ϲ�������Σ�ij�������Ϊ���˽⡰�����Ρ��Ƿ����Ա��йأ��ڻ�ɽ���ν��ڼ䣬�����ȡ��100�ˣ���������ʾ����������
�ɡ������Ρ� | ���ɡ������Ρ� | �ϼ� | |
���� | 30 | ||
�� | 10 | ||
�ϼ� | 100 |
��1������100�����У����Ա�ֲ��ȡһ������Ϊ20��������Ů��Ӧ��11�ˣ��뽫����������������������ڴ����ֱ����д���������Ҫд�����̣������ݴ������ܷ��ڷ�����ĸ��ʲ�����0.05ǰ���£���Ϊ�ɡ������Ρ������Ա��й�ϵ��
��2�����Գ�ȡ������Ƶ��Ϊ���ʣ������ν��ο��������ȡ3�����;�������Ʒ������3�����ɡ������Ρ�����ΪX����X�ķֲ��к���ѧ������ ����K2= ![]()
P��K2��k�� | 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
