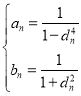题目内容
【题目】如图,已知三棱锥P-ABC中,∠ACB=90°,CB=4,AB=20,D为AB中点,M为PB中点,且△PDB是正三角形,PA⊥PC。
 .
.
(1)求证:DM∥平面PAC;
(2)求证:平面PAC⊥平面ABC;
(3)求三棱锥M-BCD的体积
【答案】(1)详见解析,(2)详见解析,(3)![]()
【解析】
试题分析:(1)证线面平行找线线平行,本题有中点条件,可利用中位线性质.即DM∥AP,写定理条件时需完整,因为若缺少DM![]() 面APC,,则DM可能在面PAC内,若缺少AP
面APC,,则DM可能在面PAC内,若缺少AP![]() 面APC,则DM与面PAC位置关系不定.(2)证面面垂直关键找线面垂直.可由面面垂直性质定理探讨,因为BC垂直AC,而AC为两平面的交线,所以应有BC垂直于平面PAC,这就是本题证明的首要目标.因为BC垂直AC,因此只需证明BC垂直平面PAC另一条直线.这又要利用线面垂直与线线垂直关系转化.首先将题目中等量关系转化为垂直条件,即DM⊥PB,从而有PA⊥PB,而PA⊥PC,所以PA⊥面PBC,因此PA⊥BC.(3)求锥的体积关键找出高,有(2)有PA⊥面PBC,因此DM为高,利用体积公式可求得
面APC,则DM与面PAC位置关系不定.(2)证面面垂直关键找线面垂直.可由面面垂直性质定理探讨,因为BC垂直AC,而AC为两平面的交线,所以应有BC垂直于平面PAC,这就是本题证明的首要目标.因为BC垂直AC,因此只需证明BC垂直平面PAC另一条直线.这又要利用线面垂直与线线垂直关系转化.首先将题目中等量关系转化为垂直条件,即DM⊥PB,从而有PA⊥PB,而PA⊥PC,所以PA⊥面PBC,因此PA⊥BC.(3)求锥的体积关键找出高,有(2)有PA⊥面PBC,因此DM为高,利用体积公式可求得![]()
试题解析:(1)D为AB中点,M为PB中点
![]() DM∥AP
DM∥AP
又![]() DM
DM![]() 面APC,AP
面APC,AP![]() 面APC
面APC
![]() DM∥面PAC
DM∥面PAC
(2)![]() △PDB是正三角形,M为PB中点
△PDB是正三角形,M为PB中点
![]() DM⊥PB,又
DM⊥PB,又![]() DM∥AP,
DM∥AP,![]() PA⊥PB
PA⊥PB
又![]() PA⊥PC,PB
PA⊥PC,PB![]() PC=P,PA⊥面PBC
PC=P,PA⊥面PBC
又![]() BC
BC![]() 面PBC,
面PBC,![]() PA⊥BC
PA⊥BC
又![]() ∠ACB=90°,
∠ACB=90°,![]() BC⊥AC
BC⊥AC
又![]() AC
AC![]() PA=A,
PA=A,![]() BC⊥面PAC
BC⊥面PAC
又![]() BC
BC![]() 面ABC,
面ABC,![]() 面PAC⊥面ABC
面PAC⊥面ABC
(3)![]() AB=20,D为AB中点,AP⊥面PBC
AB=20,D为AB中点,AP⊥面PBC
![]() PD=10
PD=10
又![]() △PDB为正三角形,
△PDB为正三角形,![]() DM=5
DM=5![]()
又![]() BC=4,PB=10,
BC=4,PB=10,![]() PC=2
PC=2![]()
![]() S△PBC=
S△PBC=![]()
![]()
![]()

 ABC考王全优卷系列答案
ABC考王全优卷系列答案【题目】某班同学利用国庆节进行社会实践,对![]() 岁的人群随机抽取
岁的人群随机抽取![]() 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低硕族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低硕族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 低碳族的人数 | 占本组的频率 |
第一组 |
| 120 | 0.6 |
第二组 |
| 195 |
|
第三组 |
| 100 | 0.5 |
第四组 |
|
| 0.4 |
第五组 |
| 30 | 0.3 |
第六组 |
| 15 | 0.3 |
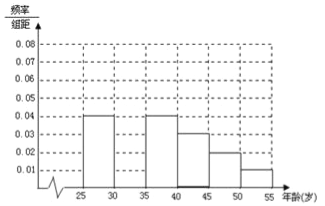
(1)补全频率分布直方图并求![]() 的值(直接写结果);
的值(直接写结果);
(2)从年龄段在![]() 的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中至少有1人年龄在
的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中至少有1人年龄在![]() 岁的概率.
岁的概率.