题目内容
19.证明:若函数y=f(x),x∈R满足f(x)=f(x-a)+f(x+a)(常数a∈R+),则f(x)是周期函数,且6a是它的一个周期.分析 由f(x)=f(x-a)+f(x+a)得f(x+a)=f(x)+f(x+2a),两式相加得f(x+2a)=-f(x-a),令x取x+a、x+3a分别化简,由函数的周期性的定义即可证明结论成立.
解答 证明:因为f(x)=f(x-a)+f(x+a),
所以f(x+a)=f(x)+f(x+2a),
两式相加得,f(x+2a)=-f(x-a),
令x取x+a得,f(x+3a)=-f(x),
令x取x+3a得,f(x+6a)=f([x+3a)+3a]=-f(x+3a)=f(x),
即f(x+6a)=f(x),又常数a∈R+,
所以f(x)是周期函数,且周期为6a.
点评 本题考查函数周期性的定义以及判断,考查赋值法的应用,化简、变形能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.下列条件,能使sinα+cossα>1成立的是( )
| A. | 0<α<π | B. | 0<α<$\frac{3π}{2}$ | C. | 0<α<$\frac{π}{2}$ | D. | $\frac{π}{4}$≤α≤$\frac{π}{2}$ |
8.一个几何体的三视图如图所示,则这个几何体的体积为( )
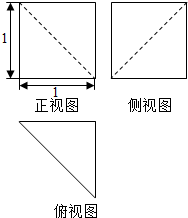

| A. | $\frac{5}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |