题目内容
14.已知△ABC的内角为A、B、C的所对的边分别为a,b,c,且A、B、C成等差数列.且△ABC的面积为4√3,则2a+3c的最小值为8√6.分析 由条件利用等差数列的定义求得B=π3,再利用三角形的面积公式求得ac=16,再利用基本不等式求得2a+3c的最小值.
解答 解:△ABC中,A、B、C成等差数列,故2B=A+C,故B=π3,A+C=2π3.
∵△ABC的面积为12•ac•sinB=4√3,∴ac=16,
∴2a+3c≥2√6ac=8√6,当且仅当2a=3c时,取等号,
故2a+3c的最小值为8√6,
故答案为:8√6.
点评 本题主要考查等差数列的定义,三角形的面积公式,基本不等式的应用,属于基础题.

练习册系列答案
相关题目
12.在正方体ABCD-A′B′C′D′中,过对角线BD′的一个平面交AA′于E、交CC′于F,则以下结论中错误的是( )
| A. | 四边形BFD′E一定是平行四边形 | |
| B. | 四边形BFD′E有可能是正方形 | |
| C. | 四边形BFD′E有可能是菱形 | |
| D. | 四边形BFD′E在底面投影一定是正方形 |

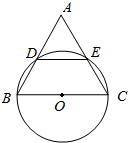 如图,以⊙O的直径BC为一边作等边△ABC,AB、AC交⊙O于点DE,求证:BD=DE=EC.
如图,以⊙O的直径BC为一边作等边△ABC,AB、AC交⊙O于点DE,求证:BD=DE=EC.