题目内容
(本小题满分14分)
已知:数列{ }的前n项和为
}的前n项和为 ,满足
,满足 =
=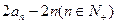
(Ⅰ)证明数列{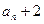 }是等比数列.并求数列{
}是等比数列.并求数列{ }的通项公式
}的通项公式 =?
=?
(Ⅱ)若数列{ }满足
}满足 =log2(
=log2(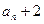 ),而
),而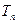 为数列
为数列 的前n项和,求
的前n项和,求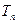 =?
=?
(Ⅰ)
(Ⅱ)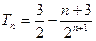
解析

练习册系列答案
相关题目
题目内容
(本小题满分14分)
已知:数列{ }的前n项和为
}的前n项和为 ,满足
,满足 =
=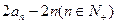
(Ⅰ)证明数列{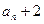 }是等比数列.并求数列{
}是等比数列.并求数列{ }的通项公式
}的通项公式 =?
=?
(Ⅱ)若数列{ }满足
}满足 =log2(
=log2(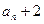 ),而
),而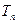 为数列
为数列 的前n项和,求
的前n项和,求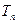 =?
=?
(Ⅰ)
(Ⅱ)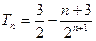
解析
