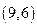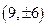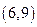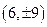题目内容
已知抛物线 的一个内接三角形的一顶点在原点,三条高线都通过抛物线的焦点,求这个三角形的外接圆的方程。
的一个内接三角形的一顶点在原点,三条高线都通过抛物线的焦点,求这个三角形的外接圆的方程。
 的一个内接三角形的一顶点在原点,三条高线都通过抛物线的焦点,求这个三角形的外接圆的方程。
的一个内接三角形的一顶点在原点,三条高线都通过抛物线的焦点,求这个三角形的外接圆的方程。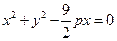
设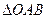 为抛物线
为抛物线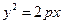 的内接三角形,因为垂心在焦点
的内接三角形,因为垂心在焦点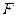 上,所以
上,所以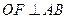 ,即
,即 轴,垂足为
轴,垂足为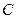 ,且由抛物线的对称性可知,
,且由抛物线的对称性可知,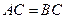 ,设
,设 所在的直线方程为
所在的直线方程为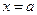 ,所以
,所以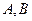 两点的坐标分别为
两点的坐标分别为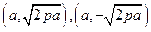 ,因为
,因为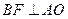 ,所以
,所以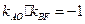 ,∴
,∴ ,得
,得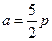 ,∵所求三角形外接圆过原点,故可设所求圆的方程为
,∵所求三角形外接圆过原点,故可设所求圆的方程为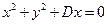 ,点
,点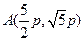 在圆上,代入A点的坐标,得
在圆上,代入A点的坐标,得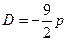 ,∴所求
,∴所求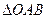 的外接圆的方程为
的外接圆的方程为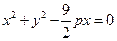 。
。
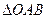 为抛物线
为抛物线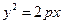 的内接三角形,因为垂心在焦点
的内接三角形,因为垂心在焦点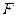 上,所以
上,所以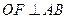 ,即
,即 轴,垂足为
轴,垂足为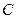 ,且由抛物线的对称性可知,
,且由抛物线的对称性可知,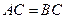 ,设
,设 所在的直线方程为
所在的直线方程为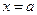 ,所以
,所以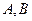 两点的坐标分别为
两点的坐标分别为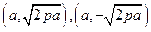 ,因为
,因为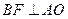 ,所以
,所以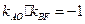 ,∴
,∴ ,得
,得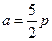 ,∵所求三角形外接圆过原点,故可设所求圆的方程为
,∵所求三角形外接圆过原点,故可设所求圆的方程为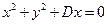 ,点
,点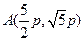 在圆上,代入A点的坐标,得
在圆上,代入A点的坐标,得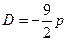 ,∴所求
,∴所求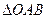 的外接圆的方程为
的外接圆的方程为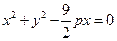 。
。
练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
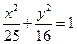 的中心为顶点,左准线为准线的抛物线与已知曲线右准线交于
的中心为顶点,左准线为准线的抛物线与已知曲线右准线交于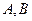 两点,则
两点,则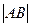 = 。
= 。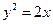 上,且与
上,且与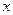 轴和该抛物线的准线都相切的一个圆的方程是( )
轴和该抛物线的准线都相切的一个圆的方程是( )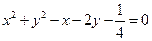
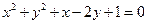

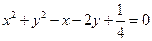
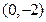 的直线与抛物线
的直线与抛物线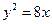 交于
交于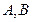 两点,若线段
两点,若线段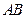 中点的横坐标为
中点的横坐标为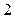 ,求
,求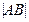 。
。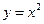 上到直线
上到直线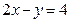 的距离最短的点的坐标是( )
的距离最短的点的坐标是( )



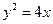 上一点
上一点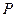 到焦点
到焦点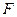 的距离是
的距离是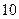 ,则
,则