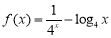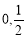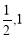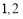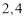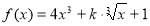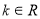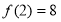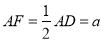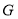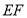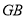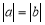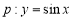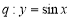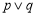题目内容
如图,在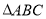 中,
中,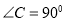 ,
,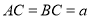 ,点
,点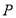 在边
在边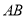 上,设
上,设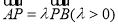 ,过点
,过点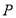 作
作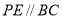 交
交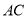 于
于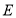 ,作
,作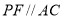 交
交 于
于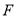 。沿
。沿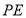 将
将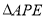 翻折成
翻折成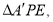 使平面
使平面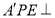 平面
平面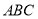 ;沿
;沿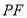 将
将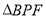 翻折成
翻折成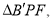 使平面
使平面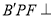 平面
平面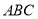 .
.
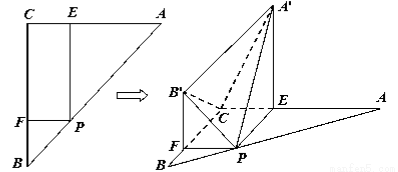
(1)求证: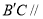 平面
平面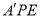 ;
;
(2)是否存在正实数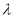 ,使得二面角
,使得二面角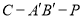 的大小为
的大小为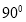 ?若存在,求出
?若存在,求出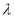 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1)证明见详解;(2)不存在,理由见解析.
【解析】
试题分析:(1)以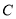 为坐标原点,以
为坐标原点,以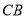 、
、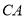 分别为
分别为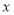 轴、
轴、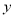 轴建立空间直角坐标系,然后通过证明向量
轴建立空间直角坐标系,然后通过证明向量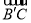 与平面平面
与平面平面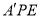 的法向量垂直;本小题也可考虑通过证明平面
的法向量垂直;本小题也可考虑通过证明平面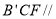 平面
平面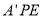 来证明;(2)由条件知二面角
来证明;(2)由条件知二面角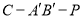 为直二面角,因此可通过两个半平面的法向量互相垂直,即其数量积为
为直二面角,因此可通过两个半平面的法向量互相垂直,即其数量积为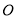 通过建立方程来解决.
通过建立方程来解决.
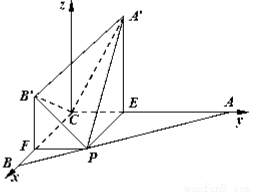
试题解析:(1)法一:以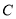 为原点,
为原点,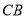 所在直线为
所在直线为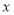 轴,
轴,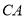 所在直线为
所在直线为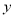 轴,过
轴,过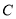 且垂直于平面
且垂直于平面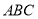 的直线为
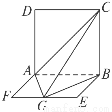
的直线为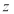 轴,建立空间直角坐标系,如图,
轴,建立空间直角坐标系,如图,
则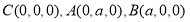 设
设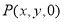 ,
,
由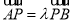
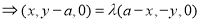
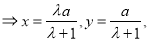
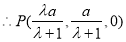 ,
,
从而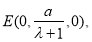
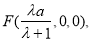 于是
于是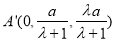 ,
,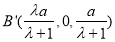 ,
,
平面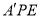 的一个法向量为
的一个法向量为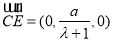 ,
,
又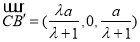 ,
,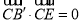 ,从而
,从而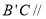 平面
平面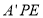 .
.
法二:因为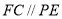 ,
,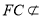 平面
平面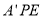 ,所以
,所以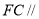 平面
平面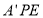 ,因为平面
,因为平面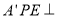 平面
平面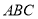 ,且
,且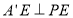 ,所以
,所以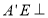 平面
平面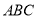 .同理,
.同理,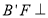 平面
平面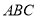 ,所以
,所以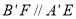 ,从而
,从而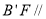 平面
平面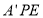 .所以平面
.所以平面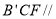 平面
平面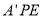 ,从而
,从而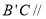 平面
平面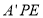 .
.
(2)【解析】
由(1)中解法一有: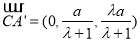 ,
,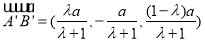 ,
,
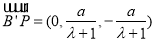 。可求得平面
。可求得平面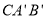 的一个法向量
的一个法向量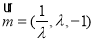 ,平面
,平面 的一个法向量
的一个法向量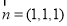 ,由
,由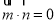 ,即
,即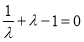 ,又
,又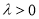 ,
,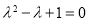 ,由于
,由于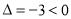 ,
,
所以不存在正实数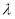 ,使得二面角
,使得二面角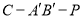 的大小为
的大小为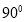 .
.
考点:1、空间向量的应用;2、面角;3、直线、平面的平行关系;4、探索性问题

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目