题目内容
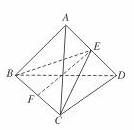
棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图所示,则图中三角形(正四面体的截面)的面积是( )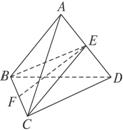
A.
B.
C.
D.
解析:找出截面三角形与正四面体的关系,利用其关系求面积.
如图,由题意知截面与棱的交点为棱AD的中点E,所以EC=,EF为△EBC的高,F为BC的中点,则EF=,S△BCE=BC·EF=.
答案:C
练习册系列答案
发散思维新课堂系列答案
相关题目
棱长为2的正四面体的四个顶点都在同一个球面上，若过该球球心的一个截面如图，则图中三角形（正四面体的截面）的面积是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
棱长为
的正四面体的外接球的体积为（ ）
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
B．
C．
D．