题目内容
【题目】已知函数f（x）=lnx﹣x3与g（x）=x3﹣ax的图象上存在关于x轴的对称点，e为自然对数的底数，则实数a的取值范围是（ ）
A.（﹣∞，e）
B.（﹣∞，e]
C.（﹣∞， 
）
D.（﹣∞， ]
【答案】D
【解析】解：函数f（x）=lnx﹣x3与g（x）=x3﹣ax的图象上存在关于x轴的对称点， ∴f（x）=﹣g（x）有解，
∴lnx﹣x3=﹣x3+ax，
∴lnx=ax，在（0，+∞）有解，
分别设y=lnx，y=ax，
若y=ax为y=lnx的切线，
∴y′= 
，
设切点为（x0 ， y0），
∴a= 
，ax0=lnx0 ，
∴x0=e，
∴a= 
，
结合图象可知，a≤ ．
故选：D．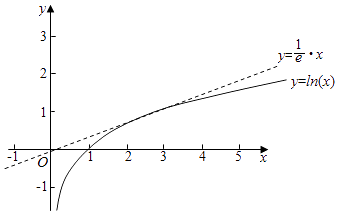
由题意可知f（x）=﹣g（x）有解，即y=lnx与y=ax有交点，根据导数的几何意义，求出切点，结合图象，可知a的范围．
练习册系列答案
相关题目
