题目内容
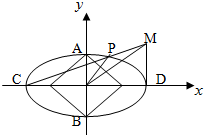 如图,已知椭圆
如图,已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆的方程;
(2)若C,D分别为长轴的左右端点,O为坐标原点,动点M满足MD⊥CD,连接CM,交椭圆于点P,判断
| OM |
| OP |
分析:(1)由于四边形F1AF2B是边长为2 的正方形,可得a=2,b=c,再利用a2=b2+c2即可解出b,c;
(2)判断
•
是定值4.设M(2,m),P(s,t),C(-2,0).则直线CM的方程为:y=
(x+2),与椭圆方程联立可得根与系数的关系,即可得出点M的坐标用m表示,再利用数量积运算即可得出
•
是定值.
(2)判断
| OM |
| OP |
| m |
| 4 |
| OM |
| OP |
解答:解:(1)∵四边形F1AF2B是边长为2 的正方形,∴a=2,b=c,
∵a2=b2+c2,∴b=c=
.
∴椭圆的方程为
+
=1.
(2)判断
•
是定值4.下面给出证明:
设M(2,m),P(s,t),C(-2,0).
则直线CM的方程为:y=
(x+2),联立
,
化为(8+m2)x2+4m2x+4m2-32=0,
∵直线与椭圆有两个交点,∴△=16m4-4(8+m2)(4m2-32)>0,化为1>0.
∴-2×s=
,解得s=
.
∴t=
.∴M(
,
).
∴
•
=(2,m)•(
,
)=
+
=4为定值.
∵a2=b2+c2,∴b=c=
| 2 |
∴椭圆的方程为
| x2 |
| 4 |
| y2 |
| 2 |
(2)判断
| OM |
| OP |
设M(2,m),P(s,t),C(-2,0).
则直线CM的方程为:y=
| m |
| 4 |
|
化为(8+m2)x2+4m2x+4m2-32=0,
∵直线与椭圆有两个交点,∴△=16m4-4(8+m2)(4m2-32)>0,化为1>0.
∴-2×s=
| 4m2-32 |
| 8+m2 |
| 16-2m2 |
| 8+m2 |
∴t=
| 8m |
| 8+m2 |
| 16-2m2 |
| 8+m2 |
| 8m |
| 8+m2 |
∴
| OM |
| OP |
| 16-2m2 |
| 8+m2 |
| 8m |
| 8+m2 |
| 32-4m2 |
| 8+m2 |
| 8m2 |
| 8+m2 |
点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、数量积运算等基础知识与基本技能方法,属于难题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
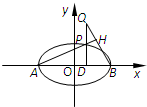 如图,已知椭圆
如图,已知椭圆 (2013•汕头一模)如图.已知椭圆
(2013•汕头一模)如图.已知椭圆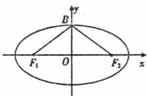 (2012•安徽模拟)如图,已知椭圆
(2012•安徽模拟)如图,已知椭圆 (2011•崇明县二模)如图,已知椭圆
(2011•崇明县二模)如图,已知椭圆 如图,已知椭圆
如图,已知椭圆