题目内容
3.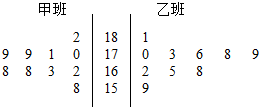 随机抽取某中学甲、乙两班各10名同学,测量他们的身高(三位整数,单位:cm),获得数据的茎叶图如图.现从两班高于175cm的所有同学中任选两人,则至少有一人来自甲班的概率为$\frac{5}{7}$.
随机抽取某中学甲、乙两班各10名同学,测量他们的身高(三位整数,单位:cm),获得数据的茎叶图如图.现从两班高于175cm的所有同学中任选两人,则至少有一人来自甲班的概率为$\frac{5}{7}$.
分析 根据茎叶图将甲、乙两组同学的身高的数据还原,利用对立事件求出概率.
解答 解:由茎叶图,得甲班的10名同学的身高分别为182 179 179 171 170 168 168 163 162 158,
乙班的10名同学的身高分别为181 170 173 176 178 179 162 165 168 159,
两班高于175cm的同学,共7人,任选两人,有${C}_{7}^{2}$=21种方法,均来自乙班的同学,共4人,任选两人,有${C}_{4}^{2}$=6种方法,∴至少有一人来自甲班的概率为1-$\frac{6}{21}$=$\frac{5}{7}$.
故答案为:$\frac{5}{7}$.
点评 本题给出茎叶图,要我们求出至少有一人来自甲班的概率,着重考查了茎叶图的认识、随机事件的概率公式等知识,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.点A(2,3,5)关于坐标平面xOy的对称点B的坐标是( )
| A. | (2,3,-5) | B. | (2,-3,5) | C. | (-2,3,5) | D. | (-2,-3,5) |
18.定义在R上的函数f(x)满足:f(-x)=f(x),且f(x+2)=f(x),当x∈[-1,0]时,f(x)=($\frac{1}{2}$)x-1,若在区间[-1,5]内函数F(x)=f(x)-logax有三个零点,则实数a的取值范围为( )
| A. | ($\frac{1}{2}$,2) | B. | (1,5) | C. | (2,3) | D. | (3,5) |
 如图,在矩形ABCD中,AB=1,BC=2,E为BC的中点,点F在DC边上,则$\overrightarrow{AE}•\overrightarrow{AF}$的最大值为( )
如图,在矩形ABCD中,AB=1,BC=2,E为BC的中点,点F在DC边上,则$\overrightarrow{AE}•\overrightarrow{AF}$的最大值为( )