题目内容
8.设命题p:{x|x2-4ax+3a2<0}(a>0),命题q:{x|1<x-1≤2}(1)如果a=1,且p∧q为真时,求实数x的取值范围;
(2)若¬p是¬q的充分不必要条件时,求实数a的取值范围.
分析 (1)当a=1时,P:{x|1<x<3},而q:{x|2<x≤3},由此利用p∧q为真,能求出实数x的取值范围.
(2)若?p是?q的充分不必要条件,表明q是p的充分不必要条件,由此能求出实数a的取值范围.
解答 (本题满分12分)
解:(1)当a>0时,{x|x2-4ax+3a2<0}
={x|(x-3a)(x-a)<0}={x|a<x<3a},
如果a=1时,命题p:{x|x2-4x+3<0},即:P:{x|1<x<3},而q:{x|2<x≤3},
因为p∧q为真,所以有{x|1<x<3}∩{x|2<x≤3}={x|2<x<3}.
故实数x的取值范围是{x|2<x≤3}.
(2)若?p是?q的充分不必要条件,表明q是p的充分不必要条件.
由(1)知,{x|2<x≤3}是{x|a<x<3a}(a>0)的真子集,
由题意得a≤2且3<3a,解得{a|1<a≤2}.
故实数a的取值范围是{a|1<a≤2}.
点评 本题考查实数的取值范围的求法,是基础题,解题时要认真审题,注意充分不必要条件、必要不充分条件、充要条件及复合命题真假判断的合理运用.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
16.2log510+log51.25=( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
13.已知f(x)是定义在R上的偶函数,并满足f(x+2)=$\frac{1}{f(x)}$,当2≤x≤3,f(x)=x,则f(25.5)等于( )
| A. | -5.5 | B. | -2.5 | C. | 2.5 | D. | 5.5 |
20.下列函数中,在(0,+∞)上是减函数的是( )
| A. | y=$\frac{1}{x}$ | B. | y=x2+1 | C. | y=2x | D. | y=x |
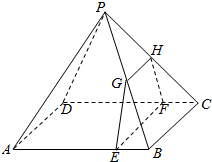 如图所示,四棱锥P-ABCD的底面是边长为8的正方形,四条侧棱长均为2$\sqrt{17}$,点G,E,F,H分别是棱PB,AB,CD,PC上共面的四点,平面GEFH⊥平面ABCD,BC∥平面GEFH.
如图所示,四棱锥P-ABCD的底面是边长为8的正方形,四条侧棱长均为2$\sqrt{17}$,点G,E,F,H分别是棱PB,AB,CD,PC上共面的四点,平面GEFH⊥平面ABCD,BC∥平面GEFH.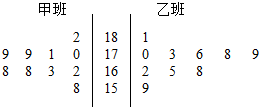 随机抽取某中学甲、乙两班各10名同学,测量他们的身高(三位整数,单位:cm),获得数据的茎叶图如图.现从两班高于175cm的所有同学中任选两人,则至少有一人来自甲班的概率为$\frac{5}{7}$.
随机抽取某中学甲、乙两班各10名同学,测量他们的身高(三位整数,单位:cm),获得数据的茎叶图如图.现从两班高于175cm的所有同学中任选两人,则至少有一人来自甲班的概率为$\frac{5}{7}$.