题目内容
13.已知直线l的方程为ρsin(θ+$\frac{π}{4}$)=$\sqrt{2}$,曲线C的方程为$\left\{\begin{array}{l}{x=cosθ}\\{y=sinθ}\end{array}\right.$(θ为参数).(1)把直线l和曲线C的方程分别化为直角坐标方程和普通方程;
(2)求曲线C上的点到直线l距离的最大值.
分析 (1)根据$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$,能求出直线l的直角坐标方程,根据sin2θ+cos2θ=1,消参后能求出曲线C的普通方程.
(2)求出圆心C到直线l:x+y-2=0的距离d=$\sqrt{2}$>1=r,直线l与圆C相离,由此得到圆上的点到直线的最大距离是圆心到直线的距离加半径.
解答 解:(1)∵直线l的方程为ρsin(θ+$\frac{π}{4}$)=$\sqrt{2}$,
∴$psinθcos\frac{π}{4}+ρcosθsin\frac{π}{4}$=$\sqrt{2}$,
∴ρsinθ+ρcosθ=2,
根据$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$,代入得:直线l的直角坐标方程为x+y-2=0.
∵曲线C的方程为$\left\{\begin{array}{l}{x=cosθ}\\{y=sinθ}\end{array}\right.$(θ为参数),
∴根据sin2θ+cos2θ=1,消参后得曲线C的普通方程是:x2+y2=1.
(2)∵曲线C:x2+y2=1是以(0,0)为圆心,以1为半径的圆,
圆心C到直线l:x+y-2=0的距离d=$\frac{|0+0-2|}{\sqrt{1+1}}$=$\sqrt{2}$>1=r,
∴直线l与圆C相离,
∴圆上的点到直线的最大距离是圆心到直线的距离加半径,
∴曲线C上的点到直线l距离的最大值为$\sqrt{2}+1$.
点评 本题考查直线的直角坐标方程和圆的普通方程的求法,考查点到直线的距离的最大值的求法,解题时要注意点到直线的距离公式的合理运用.

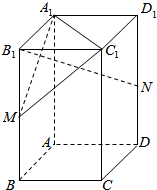 正四棱柱ABCD-A1B1C1D1中,AB=a,AA1=2a,M,N分别为BB1,DD1的中点.
正四棱柱ABCD-A1B1C1D1中,AB=a,AA1=2a,M,N分别为BB1,DD1的中点.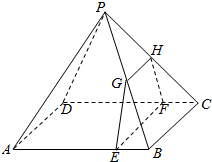 如图所示,四棱锥P-ABCD的底面是边长为8的正方形,四条侧棱长均为2$\sqrt{17}$,点G,E,F,H分别是棱PB,AB,CD,PC上共面的四点,平面GEFH⊥平面ABCD,BC∥平面GEFH.
如图所示,四棱锥P-ABCD的底面是边长为8的正方形,四条侧棱长均为2$\sqrt{17}$,点G,E,F,H分别是棱PB,AB,CD,PC上共面的四点,平面GEFH⊥平面ABCD,BC∥平面GEFH. 如图,已知PA⊥⊙O所在的平面,AB是⊙O的直径,AB=4,
如图,已知PA⊥⊙O所在的平面,AB是⊙O的直径,AB=4,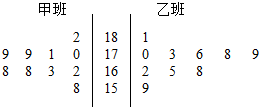 随机抽取某中学甲、乙两班各10名同学,测量他们的身高(三位整数,单位:cm),获得数据的茎叶图如图.现从两班高于175cm的所有同学中任选两人,则至少有一人来自甲班的概率为$\frac{5}{7}$.
随机抽取某中学甲、乙两班各10名同学,测量他们的身高(三位整数,单位:cm),获得数据的茎叶图如图.现从两班高于175cm的所有同学中任选两人,则至少有一人来自甲班的概率为$\frac{5}{7}$.