题目内容
18.定义在R上的函数f(x)满足:f(-x)=f(x),且f(x+2)=f(x),当x∈[-1,0]时,f(x)=($\frac{1}{2}$)x-1,若在区间[-1,5]内函数F(x)=f(x)-logax有三个零点,则实数a的取值范围为( )| A. | ($\frac{1}{2}$,2) | B. | (1,5) | C. | (2,3) | D. | (3,5) |
分析 根据条件判断函数的奇偶性和周期性,求出函数在一个周期内的解析式和图象,利用函数与方程之间的关系,利用数形结合建立不等式关系进行求解即可.
解答  解:由f(-x)=f(x)得函数f(x)是偶函数,
解:由f(-x)=f(x)得函数f(x)是偶函数,
由f(x+2)=f(x),得函数的周期为2,
若当x∈[0,1],则-x∈[-1,0],
即此时,f(-x)=($\frac{1}{2}$)-x-1=2x-1,x∈[0,1],
由F(x)=f(x)-logax=0,则f(x)=logax,
作出函数f(x)和y=logax在区间[-1,5]上的图象如图:
若0<a<1,此时两个函数图象只有1个交点,不满足条件.
若a>1,若两个函数图象只有3个交点,
则满足$\left\{\begin{array}{l}{lo{g}_{a}3<f(3)=1}\\{lo{g}_{a}5>f(5)=1}\end{array}\right.$,即$\left\{\begin{array}{l}{a>3}\\{a<5}\end{array}\right.$,解得3<a<5,
故选:D.
点评 本题主要考查函数与方程的应用,利用函数与方程的关系,转化为两个函数的交点个数问题,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
13.已知函数$f(x)=\left\{\begin{array}{l}{2^x},x≤0\\{log_3}x,x>0\end{array}\right.$,则$f[f(\frac{1}{27})]$的值为( )
| A. | $\frac{1}{8}$ | B. | 8 | C. | -8 | D. | $-\frac{1}{8}$ |
10.点P(a,3)到直线4x-3y+1=0的距离等于4,则P点的坐标是( )
| A. | (7,3) | B. | (3,3) | C. | (7,3)或(-3,3) | D. | (-7,3)或(3,3) |
8.sin(-1665°)的值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $-\frac{{\sqrt{2}}}{2}$ | D. | $-\frac{1}{2}$ |
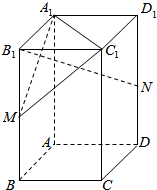 正四棱柱ABCD-A1B1C1D1中,AB=a,AA1=2a,M,N分别为BB1,DD1的中点.
正四棱柱ABCD-A1B1C1D1中,AB=a,AA1=2a,M,N分别为BB1,DD1的中点.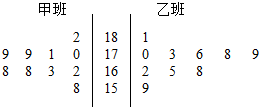 随机抽取某中学甲、乙两班各10名同学,测量他们的身高(三位整数,单位:cm),获得数据的茎叶图如图.现从两班高于175cm的所有同学中任选两人,则至少有一人来自甲班的概率为$\frac{5}{7}$.
随机抽取某中学甲、乙两班各10名同学,测量他们的身高(三位整数,单位:cm),获得数据的茎叶图如图.现从两班高于175cm的所有同学中任选两人,则至少有一人来自甲班的概率为$\frac{5}{7}$.