题目内容

如图，直线l⊥FH于H，O为FH的中点，曲线C1，C2是以F为焦点，l为准线的圆锥曲线（图中只画出曲线的一部分），那么圆锥曲线C1是______；圆锥曲线C2是______．
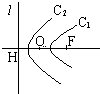
设曲线C1，C2与直线FH的交点分别为A、B，
可得曲线C1的离心率e1=
|AF|
|AH|
，
由与O为FH的中点，显然有|AF|＜|AH|，
故e1=
|AF|
|AH|
∈（0，1），故曲线C1为椭圆；
同理可得曲线C2的离心率e2=
|BF|
|BH|
，
可得e2∈（1，+∞），故曲线C2为双曲线；
故答案为：椭圆；双曲线；
练习册系列答案
相关题目
动点p（x，y）的轨迹方程为
(x-3)2+y2
-
(x+3)2+y2
=4，则判断该轨迹的形状后，可将其方程化简为对应标准方程______．
已知双曲线C：x2-
y2
4
=1，P为C上任意一点；
（1）求证：点P到双曲线C的两条渐近线的距离的乘积是一个常数；
（2）设点A（4，0），求|PA|的最小值．
F1、F2是双曲线
x2
4
-
y2
3
=1的两个焦点，过点F2作x轴的垂线交双曲线于A、B两点，则△F1AB的周长为______．
过双曲线
x2
m
-
y2
n
=1（m＞0，n＞0）上的点P（
5
，-
3
）作圆x2+y2=m的切线，切点为A、B，若
PA
•
PB
=0，则该双曲线的离心率的值是（　　）
A．4B．3C．2D．
3
双曲线的离心率为2，则双曲线的两条渐近线所成的锐角是（　　）
A．45°B．30°C．60°D．90°
设双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的右焦点为F，左，右顶点分别为A1，A2．过F且与双曲线C的一条渐近线平行的直线l与另一条渐近线相交于P，若P恰好在以A1A2为直径的圆上，则双曲线C的离心率为（　　）
A．
2
B．2C．
3
D．3
已知点P是双曲线
x2
4
-
y2
5
=1右支上一点，F是该双曲线的右焦点，点M为线段PF的中点，若|OM|=3，则点P到该双曲线右准线的距离为（　　）
A．
4
3
B．
3
4
C．
3
2
D．
2
3
双曲线
x2
36
-
y2
49
=1的渐近线方程是（　　）
A．
x
36
±
y
49
=0		B．
y
36
±
x
49
=0		C．
x
6
±
y
7
=0		D．
x
7
±
y
6
=0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网