题目内容

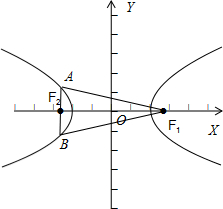
F1、F2是双曲线
x2
4
-
y2
3
=1的两个焦点，过点F2作x轴的垂线交双曲线于A、B两点，则△F1AB的周长为______．
由于双曲线的方程为
x2
4
-
y2
3
=1，则a2=4，b2=3，
则a=2，c2=a2+b2=7
由于F2是双曲线
x2
4
-
y2
3
=1的焦点，则F2是（-
7
，0）
若设A（
7
，y），则
(
7
)2
4
-
y2
3
=1，解得y=
3
2
，
故|AB|=2×
3
2
=3．
根据双曲线的定义，可知△F1AB的周长为
|F1A|+|F1B|+|AB|=|F1A|-|F2A|+|F1B|-|F2B|+2|AB|=4a+6=14．
故答案为：14
练习册系列答案
相关题目
双曲线
x2
25
-
y2
9
=1的渐近线方程是（　　）
A．y=±
25
9
x		B．y=±
5
3
x		C．y=±
25
9
x		D．y=±
3
5
x
以y=±
3
x为渐近线，且焦距为8的双曲线方程为（　　）
A．
y2
3
-x2=1
B．
y2
12
-
x2
4
=1或
x2
4
-
y2
12
=1
C．
y2
12
-
x2
4
=1
D．
y2
3
-x2=1或
x2
4
-
y2
12
=1
已知双曲线
x2
a2
-
y2
b2
=1(a＞0，b＞0)的左右焦点分别为F1，F2，P为双曲线右支一的任意一点，若
|PF1|2
|PF2|
的最小值为8a，则双曲线离心率的取值范围是（　　）
A．（0，+∞）B．（1，2]C．(1，
3
]		D．（1，3]
双曲线的渐近线方程是3x±4y=0，则双曲线的离心率等于______．
若0＜k＜a，则双曲线
x2
a2-k2
-
y2
b2+k2
=1与
x2
a2
-
y2
b2
=1有（　　）
A．相同的实轴B．相同的虚轴
C．相同的焦点D．相同的渐近线
如图，直线l⊥FH于H，O为FH的中点，曲线C1，C2是以F为焦点，l为准线的圆锥曲线（图中只画出曲线的一部分），那么圆锥曲线C1是______；圆锥曲线C2是______．
已知P在双曲线
x2
a2
-
y2
9
=1上，双曲线的一条渐近线为直线y=
3
2
x，左、右焦点分别是F1，F2．若PF1=5，则PF2的长为（　　）
A．1或9B．3或7C．8D．9
P是双曲线
x2
4
-
y2
b2
=1上一点，双曲线的一条渐近线为3x-2y=0，F1，F2分别是左、右焦点，若|PF1|=5，则P到双曲线右准线的距离是______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网