题目内容
【题目】某车间用一台包装机包装葡萄糖,每袋葡萄糖的重量是一个随机变量,它服从正态分布.当机器工作正常时,每袋葡萄糖平均重量![]() 为0.5kg,标准差
为0.5kg,标准差![]() 为0.015kg.
为0.015kg.
(1)已知包装每袋葡萄糖的成本为1元,若发现包装好的葡萄糖重量异常,则需要将该袋葡萄糖进行重新包装,假设重新包装后的葡萄糖重量正常.若某袋葡萄糖的重量![]() 满足
满足![]() ,则认为该袋葡萄糖重量正常. 问:在机器工作正常的情况下,至少包装多少袋葡萄糖才能使“至少有一袋包装好的葡萄糖重量正常”的概率大于0.98?并求出相应成本的最小期望值.
,则认为该袋葡萄糖重量正常. 问:在机器工作正常的情况下,至少包装多少袋葡萄糖才能使“至少有一袋包装好的葡萄糖重量正常”的概率大于0.98?并求出相应成本的最小期望值.
(2)某日开工后, 为检査该包装机工作是否正常, 随机地抽取它所包装的葡萄糖9袋,若抽取的9袋葡萄糖称得净重(kg)为:0.496, 0.508, 0.524, 0.519, 0.495, 0.510, 0.522, 0.513, 0.512.用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,以
,以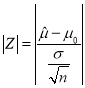 作为检验统计量,其中
作为检验统计量,其中![]() 为样本总数,
为样本总数,![]() 服从正态分布
服从正态分布![]() ,且
,且![]() .
.
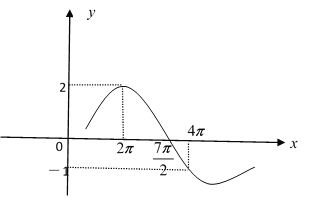
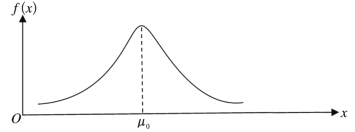
①若机器工作正常时, 每袋葡萄糖的重量服从的正态分布曲线如下图所示,且经计算得上述样本数据的标准差![]() 0.022.请在下图(机器正常工作时的正态分布曲线)中,绘制出以该样本作为估计得到的每袋葡萄糖所服从的正态分布曲线的草图.
0.022.请在下图(机器正常工作时的正态分布曲线)中,绘制出以该样本作为估计得到的每袋葡萄糖所服从的正态分布曲线的草图.
②若![]() ,就推断该包装机工作异常,这种推断犯错误的概率不超过
,就推断该包装机工作异常,这种推断犯错误的概率不超过![]() ,试以95%的可靠性估计该包装机工作是否正常.
,试以95%的可靠性估计该包装机工作是否正常.
附: 若随机变量![]() 服从正态分布:
服从正态分布:![]() ,
,![]()
![]()
参考数据:![]() ;
;![]()
【答案】(1)至少包装4袋葡萄糖,最小期望值为5.2696元;(2)①作图见解析;②在犯错误概率不超过0.05的前提下,认为该包装机工作异常,应该进行调试.
【解析】
(1)每袋葡萄糖的重量![]() 服从正态分布
服从正态分布![]() ,先根据题意求出1次包装葡萄糖重量正常的概率,则
,先根据题意求出1次包装葡萄糖重量正常的概率,则![]() 为
为![]() 次独立重复包装葡萄糖重量正常的袋数服从二项分布,根据二项分布的概率公式求出能使“至少有一袋包装的葡萄糖重量正常”的概率大于0.98的包装次数
次独立重复包装葡萄糖重量正常的袋数服从二项分布,根据二项分布的概率公式求出能使“至少有一袋包装的葡萄糖重量正常”的概率大于0.98的包装次数![]() ,此时相应的成本为
,此时相应的成本为![]() ,由期望公式
,由期望公式![]() ,求出相应成本的最小期望值;
,求出相应成本的最小期望值;
(2)①根据给出的数据求出![]() ,则
,则![]() ,
,![]() 0.022,注意
0.022,注意![]() 在
在![]() 的右侧,且峰值略低于原图像峰值,作出图象;
的右侧,且峰值略低于原图像峰值,作出图象;
②根据所给的![]() ,
, ![]() ,
,![]() ,由公式
,由公式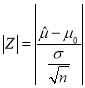 ,结合
,结合![]() ,下结论.
,下结论.
解:(1)由题意可知,机器工作正常的情况下毎袋葡萄糖的重量![]() 服从正态分布
服从正态分布
![]() ,设
,设![]() 为
为![]() 次独立重复包装葡萄糖重量正常的袋数.
次独立重复包装葡萄糖重量正常的袋数.
由![]() ,知
,知![]() 服从二项分布
服从二项分布 ![]() .
.
于是![]()
即![]()
![]() 解得:
解得:![]()
故需至少包装4袋葡萄糖,才能使“至少有一袋包装的葡萄糖重量正常”的概率大于0.98.
而![]()
故相应成本![]()
![]() ,
,
所以相应成本的最小期望值为5.2696元.
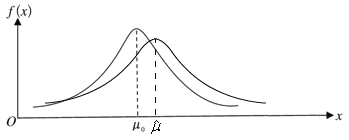
(2)①如图所示,经计算得
![]()
![]() ,(绘图时只需保证
,(绘图时只需保证![]() 在
在![]() 的右侧,且峰值略低于原图像峰值)
的右侧,且峰值略低于原图像峰值)
②易得![]() ,
, ![]() ,
,![]() ,
, 
所以在犯错误概率不超过0.05的前提下,认为该包装机工作异常,应该进行调试.

【题目】某校为举办甲、乙两项不同活动,分别设计了相应的活动方案:方案一、方案二.为了解该校学生对活动方案是否支持,对学生进行简单随机抽样,获得数据如下表:
男生 | 女生 | |||
支持 | 不支持 | 支持 | 不支持 | |
方案一 | 200人 | 400人 | 300人 | 100人 |
方案二 | 350人 | 250人 | 150人 | 250人 |
假设所有学生对活动方案是否支持相互独立.
(Ⅰ)分别估计该校男生支持方案一的概率、该校女生支持方案一的概率;
(Ⅱ)从该校全体男生中随机抽取2人,全体女生中随机抽取1人,估计这3人中恰有2人支持方案一的概率;
(Ⅲ)将该校学生支持方案的概率估计值记为![]() ,假设该校一年级有500名男生和300名女生,除一年级外其他年级学生支持方案二的概率估计值记为
,假设该校一年级有500名男生和300名女生,除一年级外其他年级学生支持方案二的概率估计值记为![]() ,试比较
,试比较![]() 与
与![]() 的大小.(结论不要求证明)
的大小.(结论不要求证明)