题目内容
9.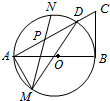 如图,AB为圆O的直径,BC为圆O的切线,连结AC交圆O于D,P为AD的中点,过P作不同于AD的弦交圆O于M、N两点,若BC=6,CD=4
如图,AB为圆O的直径,BC为圆O的切线,连结AC交圆O于D,P为AD的中点,过P作不同于AD的弦交圆O于M、N两点,若BC=6,CD=4(Ⅰ)求MP•NP的值
(Ⅱ)求证:∠C=∠AMD.
分析 (Ⅰ)利用切割线定理、相交弦定理,即可求MP•NP的值
(Ⅱ)证明∠C=∠DBA,∠DBA=∠AMD,即可证明∠C=∠AMD.
解答  (Ⅰ)解:因为BC为圆O的切线,所以BC2=CD•AC,
(Ⅰ)解:因为BC为圆O的切线,所以BC2=CD•AC,
因为BC=6,CD=4
所以AC=9,
所以AD=5,
因为P为AD的中点,
所以AP=PD=$\frac{5}{2}$
所以MP•NP=AP•PD=$\frac{25}{4}$
(Ⅱ)证明:连接BD,则∠ABC=90°,
所以∠C+∠CAB=90°,
因为AB为直径,
所以∠ADB=90°,
所以∠CAB+∠DBA=90°,
所以∠C=∠DBA,
因为∠DBA=∠AMD,
所以∠C=∠AMD.
点评 本题考查切割线定理、相交弦定理,考查学生分析解决问题的能力,正确运用切割线定理、相交弦定理是关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
17. 如果图中的程序执行后输出的结果是720,那么在程序While后面的条件应为( )
如果图中的程序执行后输出的结果是720,那么在程序While后面的条件应为( )
 如果图中的程序执行后输出的结果是720,那么在程序While后面的条件应为( )
如果图中的程序执行后输出的结果是720,那么在程序While后面的条件应为( )| A. | i>8 | B. | i>7 | C. | i≥7 | D. | i≥6 |
14.已知命题p函数f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$ax2+x有两个极值点;命题q:函数g(x)=x${\;}^{{a}^{2}-a}$在(0,+∞)上为增函数,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
1.下表给出一个等比数阵
其中每行每列都是等比数列,aij
表示第i行第j列的数.
(1)写出a34的值并求出aij的计算公式;
(2)若数列{bn}满足bn=a2n+log2a2n,求数列{bn}的前n项和Sn.
| 1 | 2 | ( ) | ( ) | ( ) | … | a1j | … |
| 3 | 6 | ( ) | ( ) | ( ) | … | a2j | … |
| ( ) | ( ) | ( ) | ( ) | ( ) | … | a3j | … |
| ai1 | ai2 | ai3 | ai4 | ai5 | … | aij | … |
| ( ) | ( ) | ( ) | ( ) | ( ) | … | … | … |
表示第i行第j列的数.
(1)写出a34的值并求出aij的计算公式;
(2)若数列{bn}满足bn=a2n+log2a2n,求数列{bn}的前n项和Sn.
18.“x<1”是“log2x<0”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
 现有四种不同颜色的染料,给如图的四个不同区域染色,每个区域只染一种颜色,相邻区域染不同的颜色,不同颜色可重复使用,则共有108种不同分染色方法(用数字作答)
现有四种不同颜色的染料,给如图的四个不同区域染色,每个区域只染一种颜色,相邻区域染不同的颜色,不同颜色可重复使用,则共有108种不同分染色方法(用数字作答)