题目内容
【题目】已知定义在![]() 上的函数
上的函数![]() .
.
(1)求![]() 单调区间;
单调区间;
(2)当![]() 时,
时,![]() 在
在![]() 上有三个零点,求
上有三个零点,求![]() 的取值范围.
的取值范围.
【答案】(1)答案不唯一,具体见解析(2)![]()
【解析】
![]() 对函数
对函数![]() 求导可得,
求导可得,![]() ,分
,分![]() ,
,![]() ,
,![]() 三种情况讨论利用导数
三种情况讨论利用导数![]() 判断函数
判断函数![]() 的单调性求单调区间即可;
的单调性求单调区间即可;
![]() 令
令![]() ,把函数
,把函数![]() 在
在![]() 上有三个零点转化为函数
上有三个零点转化为函数![]() 的图象与直线
的图象与直线![]() 在
在![]() 上有三个不同的交点,通过对函数
上有三个不同的交点,通过对函数![]() 进行求导判断其单调性并求极值,得到关于
进行求导判断其单调性并求极值,得到关于![]() 的不等式,解不等式即可.
的不等式,解不等式即可.
![]() 由题意知,
由题意知,![]() ,
,
令![]() 得
得![]() 或
或![]() ,
,
当![]() 时,
时,![]() 恒成立,
恒成立,![]() 函数
函数![]() 的单调增区间为
的单调增区间为![]() ;
;
当![]() 时由
时由![]() ,得
,得![]() 或
或![]() ;由
;由![]() ,得
,得![]() ;
;
![]() 函数
函数![]() 的单调减区间为
的单调减区间为![]() ,单调增区间为
,单调增区间为![]() ,
,![]() ;
;
当![]() 时由
时由![]() ,得
,得![]() 或
或![]() ;由
;由![]() ,得
,得![]() ;
;
![]() 函数
函数![]() 的单调减区间为
的单调减区间为![]() ,单调增区间为
,单调增区间为![]() ,
,![]() ;
;
综上可知,当![]() 时,函数
时,函数![]() 的单调增区间为
的单调增区间为![]() ;
;
当![]() 时函数
时函数![]() 的单调减区间为
的单调减区间为![]() ,单调增区间为
,单调增区间为![]() ,
,![]() ;
;
当![]() 时函数
时函数![]() 的单调减区间为
的单调减区间为![]() ,单调增区间为
,单调增区间为![]() ,
,![]() ;
;
![]() 令
令![]() ,则
,则![]() ,
,
则![]() ,令
,令![]() ,解得
,解得![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 或
或![]() 时,
时,![]() ,
,
![]() 函数
函数![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以当![]() 时,函数
时,函数![]() 有极大值为
有极大值为![]() ,
,
当![]() 时,函数
时,函数![]() 有极小值为
有极小值为![]() ,
,
使函数![]() 在
在![]() 上有三个零点,
上有三个零点,
即直线![]() 和函数
和函数![]() 有三个不同的交点,
有三个不同的交点,
由![]() 单调性,只需满足
单调性,只需满足![]() ,
,
即![]() ,解得
,解得![]() ,
,
所以实数![]() 的取值范围是
的取值范围是![]() .
.

 发散思维新课堂系列答案
发散思维新课堂系列答案【题目】随着手机的发展,“微信”逐渐成为人们交流的一种形式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如下表.
年龄 (单位:岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(1)若以“年龄45岁为分界点”,由以上统计数据完成下面2×2列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(2)若从年龄在[55,65)的被调查人中随机选取2人进行追踪调查,求2人中至少有1人不赞成“使用微信交流”的概率.
参考数据:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2=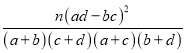 ,其中n=a+b+c+d.
,其中n=a+b+c+d.