题目内容
已知椭圆| x2 | 2 |
(1)当直线l与椭圆有公共点时,求实数m的取值范围;
(2)若直线l过椭圆右焦点,并与椭圆交于A、B两点,求弦AB之长.
分析:(1)当直线l与椭圆有公共点时,两方方程联立,消去一个未知数,得到的关于另一个未知数的一元二次方程中,△≥0,即可得到m的范围.
(2)先求出过椭圆右焦点的直线方程,在于椭圆方程联立,消去y,得到关于x的一元二次方程,求两根之和,两根之积,再利用弦长公式求弦AB之长.
(2)先求出过椭圆右焦点的直线方程,在于椭圆方程联立,消去y,得到关于x的一元二次方程,求两根之和,两根之积,再利用弦长公式求弦AB之长.
解答:解:(1)由
消y得,3x2+4mx+2m2-2=0
由于直线l与椭圆有公共点∴△=16m2-12(2m2-2)≥0,得m2≤3
故-
≤m≤
(2)设A(x1,y1),B(x2,y2),直线l过椭圆右焦点(1,0)
此时直线l:y=x-1代入椭圆方程,得3x2-4x=0
故x=0或x=
,,有|AB|=
|x1-x2|=
|
由于直线l与椭圆有公共点∴△=16m2-12(2m2-2)≥0,得m2≤3
故-
| 3 |
| 3 |
(2)设A(x1,y1),B(x2,y2),直线l过椭圆右焦点(1,0)
此时直线l:y=x-1代入椭圆方程,得3x2-4x=0
故x=0或x=
| 4 |
| 3 |
| 12+12 |
| 4 |
| 3 |
| 2 |
点评:本题考查了直线与椭圆位置关系的判断,以及弦长公式的应用,属于基础题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
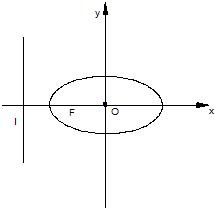 已知椭圆
已知椭圆 已知椭圆
已知椭圆