题目内容
已知椭圆| x2 | 2 |
分析:欲证直线AC经过线段EF的中点,分两类讨论:①若AB垂直于x轴,②若AB不垂直于x轴,对于第一种特殊情况比较简单,直接验证即可;对于第二种情况,记A(x1,y1)和B(x2,y2),求出直线AN,CN的斜率看它们是不是相等,若相等,则可得A、C、N三点共线.即可证得直线AC经过线段EF的中点N.
解答:证明:依设,得椭圆的半焦距c=1,右焦点为F(1,0),
右准线方程为x=2,点E的坐标为(2,0),
EF的中点为N(
,0)(3分)
若AB垂直于x轴,
则A(1,y1),B(1,-y1),C(2,-y1),
∴AC中点为N(
,0),
即AC过EF中点N.
若AB不垂直于x轴,由直线AB过点F,
且由BC∥x轴知点B不在x轴上,
故直线AB的方程为y=k(x-1),k≠0.
记A(x1,y1)和B(x2,y2),
则C(2,y2)且x1,
x2满足二次方程
+k2(x-1)2=1
即(1+2k2)x2-4k2x+2(k2-1)=0,
∴x1+x2=
,x1x2=
(10分)
又x21=2-2y21<2,得x1-
≠0,
故直线AN,CN的斜率分别为
k1=
=
k2=
=2k(x2-1)
∴k1-k2=2k•
∵(x1-1)-(x2-1)(2x1-3)=3(x1+x2)-2x1x2-4
=
[12k2-4(k2-1)-4(1+2k2)]=0
∴k1-k2=0,即k1=k2,故A、C、N三点共线.
所以,直线AC经过线段EF的中点N.(14分)
右准线方程为x=2,点E的坐标为(2,0),
EF的中点为N(
| 3 |
| 2 |
若AB垂直于x轴,
则A(1,y1),B(1,-y1),C(2,-y1),
∴AC中点为N(
| 3 |
| 2 |
即AC过EF中点N.
若AB不垂直于x轴,由直线AB过点F,
且由BC∥x轴知点B不在x轴上,
故直线AB的方程为y=k(x-1),k≠0.
记A(x1,y1)和B(x2,y2),
则C(2,y2)且x1,
x2满足二次方程
| x2 |
| 2 |
即(1+2k2)x2-4k2x+2(k2-1)=0,
∴x1+x2=
| 4k2 |
| 1+2k2 |
| 2(k2-1) |
| 1+2k2 |
又x21=2-2y21<2,得x1-
| 3 |
| 2 |
故直线AN,CN的斜率分别为
k1=
| y1 | ||
x1-
|
| 2k(x1-1) |
| 2x1-3 |
| y2 | ||
2-
|
∴k1-k2=2k•
| (x1-1)-(x2-1)(2x1-3) |
| 2x1-3 |
∵(x1-1)-(x2-1)(2x1-3)=3(x1+x2)-2x1x2-4
=
| 1 |
| 1+2k2 |
∴k1-k2=0,即k1=k2,故A、C、N三点共线.
所以,直线AC经过线段EF的中点N.(14分)
点评:直线与圆锥曲线联系在一起的综合题在高考中多以高档题、压轴题出现,主要涉及位置关系的判定,弦长问题、最值问题、对称问题、轨迹问题等,突出考查了数形结合、分类讨论、函数与方程、等价转化等数学思想方法,要求考生分析问题和解决问题的能力、计算能力较高,起到了拉开考生“档次”,有利于选拔的功能

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
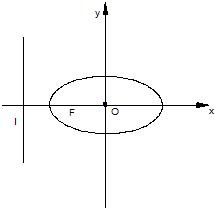 已知椭圆
已知椭圆 已知椭圆
已知椭圆