题目内容
(本小题满分12分)
已知Sn为数列{an}的前n项和,a1=9,Sn=n2an-n2(n-1),设bn=
(1)求证:bn-bn-1="n" (n≥2,n∈N).
(2)求 的最小值.
的最小值.
(1)运用通项公式与前n项和的关系来分析证明递推关系。
(2) 
解析试题分析:解:(1)


 --------------(6分)
--------------(6分)
(2)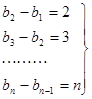
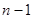 个式子相加得
个式子相加得
又

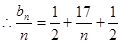
当 时,
时,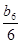 最小,值为
最小,值为 --------------------(12分)
--------------------(12分)
考点:数列的递推关系以及最值
点评:解决该试题的关键是能利用前n项和公式,根据整体的思想得到第n项,进而得到递推关系,同时能根据已知的累加法来得到数列的最值,属于基础题。

练习册系列答案
相关题目
 满足:
满足: ,
, .
. .
.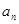 及
及 (n
(n N*),求数列
N*),求数列 的前n项和
的前n项和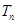 .
. ,前
,前 项的和为
项的和为 ,
, =2550.
=2550. 及
及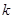 的值;
的值; 
 ,其中
,其中 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列; 是公差为
是公差为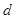 的等差数列;
的等差数列; 是公差为
是公差为 的等差数列(
的等差数列( ).
). = 30,求
= 30,求 是公差为
是公差为 关于
关于 N
N );
);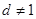 ,试用
,试用
 满足:
满足: ,
, ,
, .
. 及
及 (n
(n N*),求数列
N*),求数列 的前n项和
的前n项和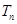 .
. }的前n项和为
}的前n项和为 ,已知
,已知 ,
, .
.
 ,求数列{
,求数列{ }的前项和
}的前项和 .
. 的前
的前 项和为
项和为 ,且
,且 .
. 满足:
满足: 求数列
求数列 求数列
求数列 的前
的前 .
. 是公差不为0的等差数列
是公差不为0的等差数列 的前n项和,且
的前n项和,且 成等比数列。
成等比数列。 ,求
,求 ,
, 是数列
是数列 的前n项和,求使得
的前n项和,求使得 对所有
对所有 都成立的最小正整数
都成立的最小正整数 。
。 是等差数列,
是等差数列,
 ,求数列
,求数列 的前n项和Sn.
的前n项和Sn.