题目内容
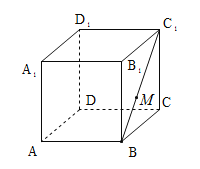
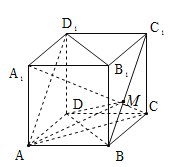
【题目】如图,在正方体![]() 中,点
中,点![]() 在面对角线
在面对角线![]() 上运动,则下列四个结论:
上运动,则下列四个结论:
①![]()
②![]()
③![]() 平面
平面![]()
④三棱锥![]() 的体积是定值
的体积是定值
其中正确结论的个数有( )个.
A.1B.2
C.3D.4
【答案】D
【解析】
①:根据正方体的性质,结合线面垂直的判定定理,可以证明出![]() 平面
平面![]() ,最后进行判断即可;
,最后进行判断即可;
②:利用正方体的性质,结合线面垂直的判定定理和性质可以证明出![]() 平面
平面![]() ,最后进行判断即可;
,最后进行判断即可;
③:利用正方体的性质,结合面面平行的判定定理和面面平行的性质进行判断即可;
④:同③得到的线面平行,结合三棱锥的体积公式进行判断即可.
①:由正方体的性质可知:![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,所以有
,所以有![]() ,因为正方体的侧面是正方形,所以有
,因为正方体的侧面是正方形,所以有![]() ,而
,而![]() ,所以有
,所以有![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,所以
,所以![]() ,故本结论是正确的;
,故本结论是正确的;
②:由正方体的性质可知:![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,所以有
,所以有![]() ,因为正方体的底面是正方形,所以有
,因为正方体的底面是正方形,所以有![]() ,而
,而![]() ,所以有
,所以有![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,所以
,所以![]() ,同理可证明出
,同理可证明出![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,因此
,因此![]() ,故本结论是正确的;
,故本结论是正确的;
③:因为![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,同理
,同理![]() 平面
平面![]() ,而
,而![]() ,因此平面
,因此平面![]() 平面
平面![]() ,因为
,因为![]() 平面
平面![]() ,所以有
,所以有![]() 平面
平面![]() ,故本命题是正确的;
,故本命题是正确的;
④:同③得: ![]() 平面
平面![]() ,所以点
,所以点![]() 在面对角线
在面对角线![]() 上运动,点
上运动,点![]() 到平面
到平面![]() 的距离不变,设为
的距离不变,设为![]() ,因此有
,因此有![]() ,显然三棱锥
,显然三棱锥
![]() 的体积是定值,故本命题是正确的.
的体积是定值,故本命题是正确的.
故选:D

练习册系列答案
相关题目
【题目】根据调查,某学校开设了“街舞”、“围棋”、“武术”三个社团,三个社团参加的人数如下表所示:
社团 | 街舞 | 围棋 | 武术 |
人数 | 320 | 240 | 200 |
为调查社团开展情况,学校社团管理部采用分层抽样的方法从中抽取一个容量为n的样本,已知从“围棋”社团抽取的同学比从“街舞”社团抽取的同学少2人.
(1)求三个社团分别抽取了多少同学;
(2)若从“围棋”社团抽取的同学中选出2人担任该社团活动监督的职务,已知“围棋”社团被抽取的同学中有2名女生,求至少有1名女同学被选为监督职务的概率。