题目内容
4. 如图,在长方体ABCD-A1B1C1D1中,点E,F分别是棱AB,BC的中点,点E1,F1分别是棱A1D1,C1D1的中点.求证:EE1∥FF1.
如图,在长方体ABCD-A1B1C1D1中,点E,F分别是棱AB,BC的中点,点E1,F1分别是棱A1D1,C1D1的中点.求证:EE1∥FF1.
分析 连结EF,E1F1,A1C1,AC,由长方体ABCD-A1B1C1D1中结合点E,F分别是棱AB,BC的中点,只要判断四边形EFF1E1为平行四边形.
解答  证明:连结EF,E1F1,A1C1,AC,
证明:连结EF,E1F1,A1C1,AC,
由长方体ABCD-A1B1C1D1中知,AC∥A1C1,
∵点E,F分别是棱AB,BC的中点,
∴由三角形中位线定理得:EF∥$\frac{1}{2}AC$,
同理E1F1∥$\frac{1}{2}{A_1}{C_1}$,…(7分)
∴EF∥E1F1,则四边形EFF1E1为平行四边形,
故EE1∥FF1.…(14分)
点评 本题考查了长方体的性质运用;属于基础题.

练习册系列答案
相关题目
19.如图,在正方体ABCD-A1B1C1D1中,下列结论正确的是( )


| A. | A1C1∥AD | B. | C1D1⊥AB | ||
| C. | AC1与CD成45°角 | D. | A1C1与B1C成60°角 |
16.若一个正三棱柱的三视图如图所示,则这个正三棱柱的体积为( )


| A. | 8 | B. | $\frac{8}{3}$$\sqrt{3}$ | C. | 8$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
 如图,△ABC中,∠ACB=90°,D是AC上一点,以AD为直径作⊙O交AB于点G
如图,△ABC中,∠ACB=90°,D是AC上一点,以AD为直径作⊙O交AB于点G 已知一个几何体的三视图如图所示,则这个几何体的体积为$\frac{22}{3}$.
已知一个几何体的三视图如图所示,则这个几何体的体积为$\frac{22}{3}$.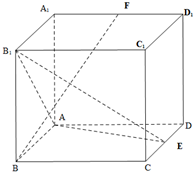 如图:在长方体ABCD-A1B1C1D1中,AB=2,BC=4,BB1=4,E是CD的中点,F是A1D1的中点.
如图:在长方体ABCD-A1B1C1D1中,AB=2,BC=4,BB1=4,E是CD的中点,F是A1D1的中点. AC=BC=$\sqrt{2}$,CD=DE=1,AB=BE=EA=2,CD⊥面ABC.
AC=BC=$\sqrt{2}$,CD=DE=1,AB=BE=EA=2,CD⊥面ABC. 在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,当D为PB的中点
在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,当D为PB的中点